Искомая площадь состоит из трех равных площадей треугольников, у которых есть высота - апофема боковой грани, нужно найти сторону основания. И тогда площадь боковой поверхности равна 3а*L/2, где а - сторона основания. Если соединить основание апофемы и и высоты пирамиды, получим проекцию апофемы на плоскость основания, и она равна (1/3) высоты треугольника, лежащего в основании. Зная апофему и угол между апофемой и высотой, найдем эту проекцию. Она равна L*sinα=а√3/2, отсюда сторона основания а =2L*sinα/√3=
2L*sinα*√3/3
Значит, площадь боковой поверхности равна (3*2L*sinα*√3/3)*L/2=
L²*√3sinα/ед. кв./
Отрезок, соединяющий основание перпендикуляра и наклонной, проведённых из одной и той же точки, является проекцией этой наклонной. (см. рисунок в приложении).
В треугольнике боковая сторона - наклонная, его высота - перпендикуляр к прямой, содержащей другую сторону.
Высота равностороннего треугольника еще и медиана и биссектриса. Все углы равностороннего треугольника =60°. Поэтому проекция стороны - катет прямоугольного треугольника, который противолежит углу 30°. По свойству такого катета он равен половине гипотенузы. ⇒
Проекция стороны данного треугольника на прямую, содержащую другую сторону – 1:2=0,5

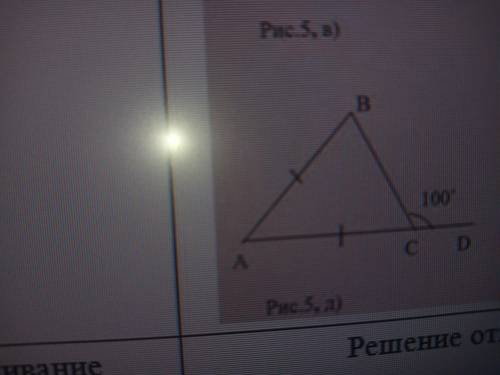
смотри ответ прост угол abc равен 80 градусам
Объяснение:
АВ=АС по условию
Угол ВСD и угол ВСА смежные
треугольник АВС равнобедренный по доказаному
АС и АВ боковые стороны треугольника АВС
ВС основание
а у равнобедреного треугольника углы при основании равны
а это значит что угол АВС равен углу АСВ
а т.к ВСD и угол ВСА смеж по правилу смежных углов
тоесть их сумма равна 180 градусам
180-100=80(ВСА)
а как я и говорил раньше угол ВСА равен углу АВС
угол ВСА= углу АВС =80 градусам