Question

с геометрией. Задачи со скай смарта. Буду благодарен за ответы.

Answer 1

Объяснение:

Решение прикрепил ниже

Answer 2

Не знаю, как здесь обозначить вектор. Пусть будет ⁻. То есть, а⁻ - вектор а.

a⁻ (-5; -10); b⁻ (2; 7).

1) a⁻ + b⁻ (-3; -3)

2) 4 · a⁻ (-20; -40)

3) -2 · a⁻ + 3 · b⁻ (16; 41)

4) -b⁻ (-2; -7)

p⁻ (-3; 4); l⁻ (1; 2)

1) p⁻ - l⁻ (-4; 2)

2) Признак коллинеарности векторов: векторы коллинеарны, когда их координаты пропорциональны. Проверяем, вектор (p⁻ - l⁻) имеет координаты (-4; 2), а вектор k - координаты (4; -2).

$\frac{-4}{4} = \frac{2}{-2}\\-1 = -1$

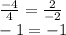
Так как их координаты пропорциональны, то эти векторы коллинеарны.

Если А (-2; 2), B (3; 5), то AB⁻ (5; 3).