
№1
1) Неверно (эти углы вертикальны)
2) Верно
3) Неверно (он прямой, по условию он равен 90°)
4) Верно (угол ВКЕ смежный с углом АКЕ, тогда их сумма равна 180°. Следовательно угол ВКЕ=180°–угол АКЕ=180°–90°=90°. Угол равный 9∆° – прямой)
ответ: 2) 4)
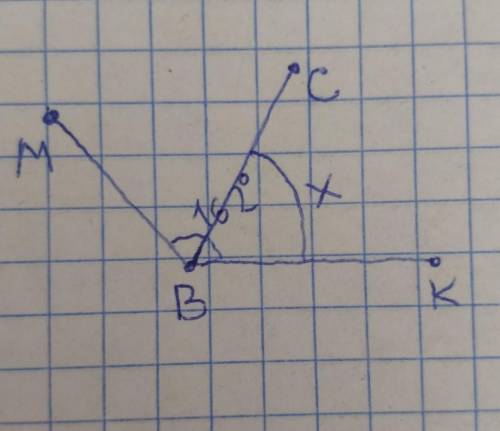
№2 (с фото)
Угол КВС – угол образованный биссектрисой и стороной угла, следовательно он будет равен половине угла, который делит данная биссектриса.
Тоесть угол КВС=угол МВК÷2=162°÷2=81°
ответ: 81°
№3
Углы CMD и BMC – смежные, значит их сумма равна 180°.
Следовательно угол СМD=180°–угол ВМС=180°–58°=122°
ответ: 122°
№4
Пусть DM=x, тогда ВМ=х+12
BD=DM+BM
Составим уравнение:
34=х+х+12
2х=22
х=11
Тогда DM=11 см, а BM=11+12=23 см
DM=11 см, а BM=11+12=23 смответ: 23 см; 11 см.
ответ:ответ, проверенный экспертом
4.0/5
13
KuOV
главный мозг
4.9 тыс. ответов
26.7 млн пользователей, получивших
Объяснение:
a)(Фото)
https://ru-static.z-dn.net/files/dd9/6dbd3d984a1b49a60897ad7ac129c92c.png
b)Тангенс острого угла прямоугольного треугольника - это отношение противолежащего катета к прилежащему.
Значит надо построить прямоугольный треугольник, отношение катетов которого равно 1:4. Угол, лежащий против меньшего катета будет искомым.
Если это не задача на построение, то можно построить треугольник по клеточкам тетради так, чтобы один катет был равен, например, одному сантиметру, а другой - 4 см. Тогда угол, лежащий против катета в 1 см - искомый. На рисунке это ∠АВО.
Если задача на построение, то
строим две перпендикулярные прямые, для этого
проводим прямую а, отмечаем на ней две произвольные точки К и Р; проводим две окружности с центрами в этих точках произвольного одинакового радиуса, большего половины отрезка КР; через точки пересечения этих окружностей Е и Н проводим прямую. ЕН⊥а. О - точка пересечения прямых.
от точки О с циркуля откладываем равные отрезки вверх один (точка А), влево - 4 (точка В).
соединяем получившиеся точки;
∠АВО - искомый.
https://ru-static.z-dn.net/files/dbc/dd6b3aac185aecfed037c2300250715f.png