
1)Все грани куба– квадраты, диагонали квадрата взаимно перпендикулярны, B1D1⊥A1C1. B1D1– проекция наклонной B1D. По теореме о трех перпендикулярах B1D ⊥ A1C1
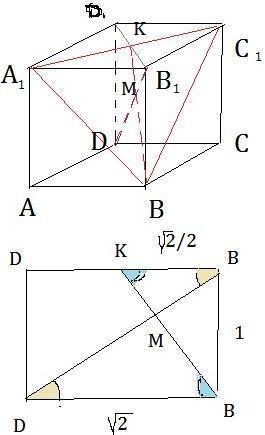
Треугольник A1BC1– равносторонний, Проведем высоту ВК (К– точка пересечения диагоналей) B1D пересекается с КВ в точке М.
Треугольники КВ1М и DBM подобны по двум углам. (см. рисунок) D1B1=DB=√2 KB1=√2/2 По теореме Пифагора B1D=√3 KB=√(3/2) KM:MB=1:2 KM:((√3/2)–KB)=1:2 KB=√6/6 B1M:MD=1:2 B1M:(√3– B1M)=1:2 B1M=√3/3
В треугольнике В1КМ B1K²=B1M²+MK² 1/2=(1/3)+(1/6) Треугольник прямоугольный угол B1MK– прямой
Итак, B1D– перпендикулярна двум пересекающимся прямым А1С1 и BK, значит перпендикулярна плоскости А1ВС1.
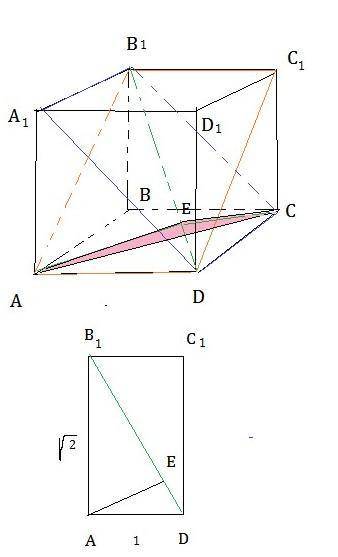
2) Плоскость АВ1С1– это плоскость АB1C1D Плоскость A1B1C– это плоскость A1B1CD
Две эти плоскости имеют общие точки B1 и D. Значит пересекаются по прямой, проходящей через эти точки.
Чтобы построить линейный угол двугранного угла проводим к прямой B1D перпендикуляры AE и EC. AE=EC– высоты прямоугольных треугольников с катетами 1 и √2 и гипотенузой √3 АЕ=ЕС=1•√2/√3=√(2/3)
Из треугольника АСЕ по теореме косинусов АС²=АЕ²+ЕС²–2•АЕ•ЕС•cos ∠AEC (√2)²=(√(2/3))²+(√(2/3))²–2•(√(2/3))•(√(2/3))•cos ∠AEC cos ∠AEC=–1/2 ∠AEC=120°
пирамида КАВС, К -вершина , в основании равносторонний треугольник АВС, О-центр основания =пересечение медиан=высот=биссектрис, проводим высоту ВН на АС, уголКВО=45, КО=высота пирамиды=4*корень3, треугольник КВО прямоугольный, уголВКО=90-уголКВО=90-45=45, треугольник КВО равнобедренный, КО=ВО=4*корень3, ВН-медиана, которая в точке пересечения делится в отношении 2/1 начиная от вершины, ВО=2 части, ОН=1 часть=ВО/2=4*корень3/2=2*корень3, ВН=ВО+ОН=4*корень3+2*корень3=6*корень3, АВ=ВС=АС=2*ВН*корень3/3=2*6*корень3*корень3/3=12, площадьАВС=АС в квадрате*корень3/4=144*корень3/4=36*корень3, объем=1/3*площадьАВС*КО=1/3*36*корень3*4*корень3=144