Объяснение:
Дано:
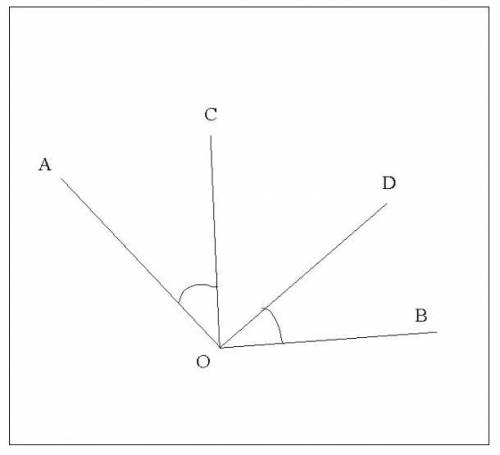
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.
Дано: трап. ABCD
AC=BD
Кут А / кут В = 4/5
Розв'язання
Якщо січна AC=BD то ця трапеція рівнобічна.
Нехай х коефіцієнт пропорційності тоді кут А =4х, а кут В=5х. Оскільки сума кутів прилеглих до бічної сторони трапеції дорівнюють 180 градусів то складемо і розв'яжемо рівняння:
4х+5х=180,
9х=180,
х=180/9
х=20
Отже кут А=4*20=80 градусів, а кут В=5*20=100градусів.
Оскільки в рівнобічних трапеціях основи рівні то кут А = куту D, а кут В = куту C, то кут D = куту А = 80 градусів, а кут C = куту В = 100 градусів
Відповідь: кут А = 80 градусів, кут В = 100 градусів, кут С = 100 градусів, кут D = 80 градусів