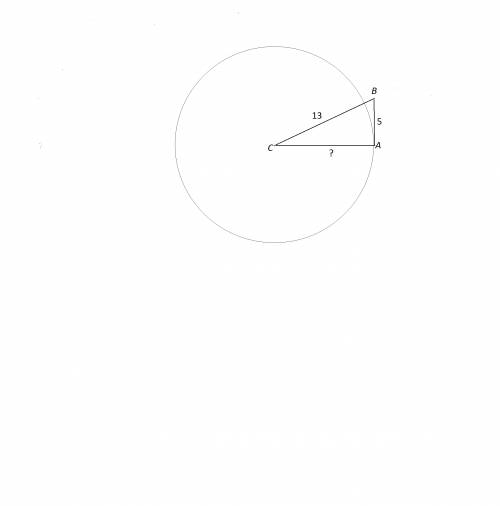
Если сделать рисунок, то будет понятно, что радиус этой окружности - катет АС данного прямоугольного треугольника.
Если окружность имеет с прямой только одну общую точку, то эта прямая - касательная к этой окружности.
Вершина угла А - точка касания.
Радиус окружности найдем по теореме Пифагора или вспомнив, что три стороны этого треугольника из так называемых троек Пифагора с отношением сторон 5:12:13.
------------------------------------------------------------------------------------------------------------------------------------
Треугольник, длины сторон которого равны пифагоровым числам, является прямоугольным. Кроме того, любой такой треугольник является героновым, то есть, все его стороны и площадь являются целыми числами.
----------------------------------------------------------------------------------------------------------------------------------------
Катет АС=12 см, и является радиусом данной окружности
Объяснение:
Высота в равнобедренном треугольнике является биссектрисой и медианой. Треугольник, образованный высотой h (неизвестный катет), боковой стороной (гипотенуза - 18 см) и половиной основания (катет - 20/2=10 см) прямоугольный. По т. Пифагора - h=√(18²-10²)=4√14 см.