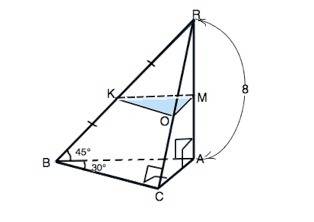
Плоскость МКО, параллельная плоскости ∆ АВС, пересекает боковые грани по прямым, параллельным сторонам основания АВС и отсекает от исходной пирамиды подобную ей пирамиду RMKO.
Площади подобных фигур относятся как квадрат отношения их линейных размеров.
k=RK:RВ=1/2 ⇒ k²=1/4
Площадь боковой поверхности пирамиды RABC равна сумме площадей её боковых граней.
S ∆ RAB=RA•AB/2
AB=RA•ctg45°=8
S ∆ RAB=8•8/2=32
S ∆ RAC=RA•AC/2
AC=AB•sin30°=8·1/2=4
S ∆ RAC=4·8/2= 16
S ∆ RCB=RC·BC/2
BC=AB·cos30•=4√3
RC по т.Пифагора=√(AC²+AR²)=√(16≠64)=4√5
S ∆ RCB=(4√5)·(4√3)/2=8√15
S бок RABC=32+16+8√15=8·(6+√15)
S бок RMKO= S бок RABC:4=2·(6+√15) ед. площади.
Если описать окружность вокруг треугольника ABC, и продлить AD до пересечения с этой окружностью в точке H1, то
DH = DH1; доказать это очень просто, если заметить, что
∠H1BD = ∠H1AC; (оба вписанных угла опираются на дугу H1C) а
∠H1AC = ∠HBD = 90° - ∠C; то есть
∠H1BD = ∠HBD; дальше очевидно.
Для хорд BC и AH1 можно записать BD*CD = AD*DH1 = AD*(AD - AH);
Если теперь достроить заданную в задаче полуокружность до полной, то BC будет хордой и в ней, и можно записать аналогично
BD*CD = MD^2; (ну, диаметр делит перпендикулярную ему хорду пополам)
Получилось
AD*(AD - AH) = MD^2; или AH = AD*(1 - (MD/AD)^2); число найдите самостоятельно.
Техническая простота решения не должна вводить в заблуждение. На самом деле полученный ответ имеет очень нетривиальную интерпретацию. Дело в том, что AH - диаметр окружности, описанной вокруг треугольника AB1C1 (где B1 и С1 - основания высот BB1 и CC1). Получается, что этот диаметр не зависит от положения точки D на BC, и от величины BC, а только от AD и MD. Слово "только" не совсем точное, поскольку величина BC не является независимой. НО результат необычный.