1) CD параллельна BE, так как накрест лежащие углы их секущей (CE) равны.
2) Учитывая то, что сумма углов выпуклого четырёхугольника равна 360 можно доказать, что перед нами параллелограмм, следовательно, по его определению, DE параллельно AH и AD параллельно FH
3) OM параллельна PK так как накрест лежащие углы их секущей (OP) равны.
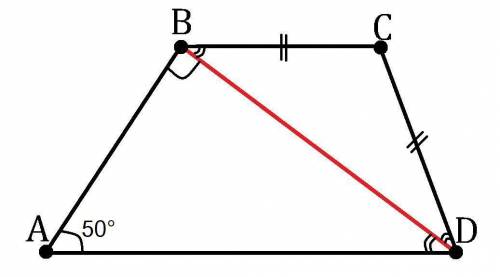
Дано: BC║AD; BD⊥AB; ∠BAD=50°; BC=DC.
Найти: ∠ABC, ∠BCD и ∠CDA.
∠BAD+∠ADB+∠DBA = 180° как сумма углов ΔBAD.
∠ADB = 180°-∠DBA-∠BAD = 180°-90°-50° = 40°
∠ADB = ∠DBC как накрест лежащие углы при параллельных прямых BC, AD и секущей DB.
∠DBC = ∠ADB = 40°.
ΔBCD - равнобедренный (по условию BC=DC), поэтому углы при его основании равны (∠DBC=∠BDC).
∠BDC = ∠DBC = 40°.
∠BCD = 180°-∠BDC-∠DBC = 180°-40°-40° = 100° т.к. сумма углов в треугольнике равна 180°.
∠ABC = ∠DBA+∠DBC = 90°+40° = 130°.
∠CDA = ∠ADB+∠BDC = 40°+40° = 80°.
ответ: 130°, 100° и 80°.
У 2 четырехугольника стороны паралельны
Так как два любых соседних угла равны 180