(МН·РН) = 4 ед.
(ОР·РК) = -2 ед.
Объяснение:
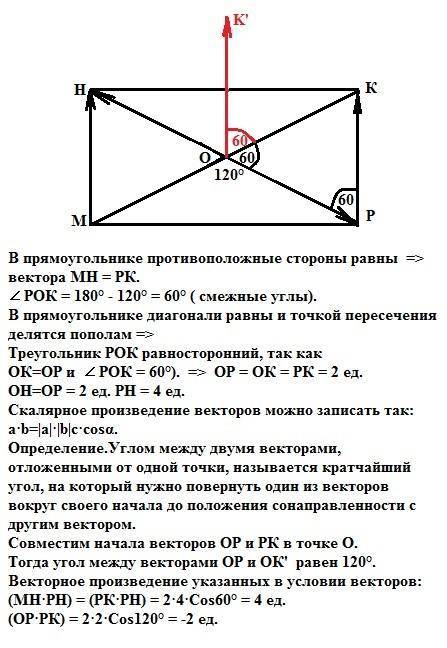
В прямоугольнике противоположные стороны равны =>
вектора МН = РК.
∠ РОК = 180° - 120° = 60° ( смежные углы).
В прямоугольнике диагонали равны и точкой пересечения делятся пополам =>
Треугольник РОК равносторонний, так как
ОК=ОР и ∠ РОК = 60°). => ОР = ОК = РК = 2 ед.
ОН=ОР = 2 ед. РН = 4 ед.
Скалярное произведение векторов можно записать так:
a·b=|a|·|b|c·сosα.
Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".
Совместим начала векторов ОР и РК в точке О. Тогда угол между векторами ОР и ОК' (вектора ОК и ОК' равны) равен 120°.
Векторное произведение указанных в условии векторов:
(МН·РН) = (РК·РН) = 2·4·Cos60° = 4 ед.
(ОР·РК) = 2·2·Cos120° = -2 ед.
Точки А (-5;-4), В (-4;3), С (-1;-1) являются вершинами треугольника АВС.
а) докажите, что треугольник АВС равнобедренный.
Длина стороны |АВ| = √((Bx - Ax)² + (By - Ay)²) = √((-4 - (-5))² + (3 - (-4))²) = √50 = 5√2 ≈ 7.07;
Длина стороны |ВC| = √((-1 - (-4))² + (-1 - 3)²) = 5;
Длина стороны |CA| = √((-5 - (-1))² + (-4 - (-1))²) = 5;
|ВC| = |CA| Это значит, что треугольник АВС равнобедренный;
б) составьте уравнение окружности, имеющий центр в точке С и проходящий через точку В. Принадлежит ли окружности точка А?
центр в точке С (-1;-1); радиус 5; уравнение окружности; (x+1)²+(y+1)²=5²;
проверяем: принадлежит ли окружности точка А; подставляем её координаты в уравнение;
((-5)+1)²+((-4)+1)²=5²; 25 = 25; точка А принадлежит окружности;
в) найдите длину медианы, проведенной к основанию треугольника.
Найдем точку F - середина стороны AB: Fx = (-5 + (-4))/2 = -4.5; Fy = (-4 + 3)/2 = -0.5;
F (-4.5; -0.5); С (-1;-1); Длина медианы CF: |CF| = √((-3.5)²+0.5²) = √12.5 = 5/√2 ≈ 3.54;
д) считая вершинами параллелограмма АВСD данные точки А, В, С, найдите координаты вершины D.
составим уравнение прямой AD, параллельной BC (с угловым коэффициентом BC), проходящую через точку A; (x+5)/-3 = (y+4)/4 ; y = -4x/3 - 32/3;
составим уравнение прямой CD, параллельной BA (с угловым коэффициентом BA), проходящую через точку C; (x+1)/1 = (y+1)/7 ; y = 7x + 6;
найдём их пересечение. -4x/3 - 32/3 = 7x + 6; x = -2; y = 7(-2) + 6; y = -8;
Это будут координаты точки D (-2;-8);
е) составьте уравнение прямой, проходящей через точки А и С.
уравнение прямой АС: (x+1)/4 = (y+1)/3; y = 3x/4 - 3/4;
Объяснение:
только так смог