1) Треугольник образованный восотой, радиусом и образующей будет прямоугольный и равнобедренный гипотенузой которого является образующая по т. Пифагора r²+r²=6,5²
2r²=42,25
r²=21,125
r≈4,6
S=πrl
S=π*4,6*6,5=29,9π≈93,9
2) воспользуемся формулой площади треугольника через синус S=1/2*a*b* sinC
a) S=1/2*2r*2r*sin 30°=1/2*2r*2r*0,5=r²
б) S=1/2*2r*2r*sin 45°=1/2*2r*2r*(√2/2)=r²√2
в) S=1/2*2r*2r*sin 60°=1/2*2r*2r*(√3/2)=r²√3
3) Sосн=πr²=8
r²=8/π
r=(2√2)/√π
так как сечение треугольник то его площадь вычисляется по формуле S=1/2*a*h
в нашем случае a это диаметр, т.е. 2r h высота конуса
1/2*(2√2)/√π*h=6
h=6*√(π/2)
Из точки находящийся на расстоянии корень с 3 см от плоскости проведен к этой плоскости две наклонные которые наклонены к плоскости под углами 45° и 60°. Найдите расстояние между основаниями наклонных если наклонные перпендикулярны.
Объяснение:
Т.к ОМ -расстояние и ОМ⊥α, то ОМ⊥ОВ и ОМ⊥ОА .
ΔОМА-прямоугольный ,∠ОАМ=45° ⇒ ∠ОМА=45° поэтому
ОМ=ОА=√3 см . Найдем по т. Пифагора МА=√(√3²+√3²)=√6 (см).
ΔОМВ -прямоугольный, ∠ОВМ=60° , sin 60=OM/MB ,√3/2=√3/МВ , МВ=2 см.
ΔОМВ -прямоугольный,по т. Пифагора АВ=√(МА²+МВ²)=√(6+4)=√10 (см)
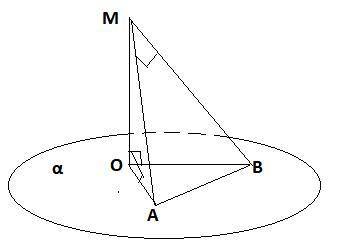
На картинке
Объяснение:
Все подробно