DE – радиус данной окружности.
Возьмём точку К (4;-7), проведем по линиям клеток DK и EK.
DK=|-5–(-7)|=|-5+7|=2
EK=|4–(-2)|=|4+2|=6
Так как углы любой клетки равны 90°, то угол DKE=90°.
Тогда по теореме Пифагора в ∆DKE:
DE²=DK²+EK²
DE²=2²+6²
DE²=4+36
DE²=40
То есть квадрат радиуса окружности равен 40.
Уравнение окружности имеет вид:
(x–a)²+(y–b)²=R²
где кординаты центра окружности (а;b), а R – радиус.
a) Центр окружности – точка D имеет кординаты (4;-5), тогда получим уравнение:
(x–4)²+(y+5)²=40
b) Центр окружности – точка E имеет кординаты (-2;-7), получим уравнение:
(х+2)²+(у+7)²=40
ответ выделен жирным шрифтом. Так как не дано какая из двух точек центр, я расписал два случая. Но вероятнее что всё-таки случай а)
Тогда ответ: (x–4)²+(y+5)²=40
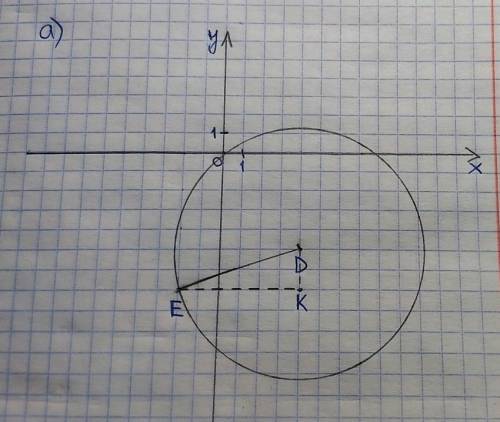
1 ) один угол 90 градусов
значит, сумма двух других 90 градусов
пусть один угол = х, тогда
2х+60 = 90
х = 15
т.е. один угол 15 градусов, другой 75 градусов
2) внутренний угол = 180-140= 40 градусам, значит и втрой угол при основании 40 градусов
третий угол = 180-40-40 = 100 градусов
3) если внешний угол 135 градусов, то внутренний = 180-135 = 45 градусов
если внешний угол 160 градусов, то внутренний = 180-160 = 20 градусов
третий угол = 180-45-20 = 115
он больше, чем 90 градусов => треугольник тупоугольный