Проведем касательные, образующие угол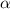 
. В точки касания проведем радиусы из центра соответствующей окружности. Теперь проведем искомое расстояние между точками касания.
Рассмотрим четырехугольник, образованный касательными и радиусами.. Из него нам нужно найти угол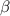 
. Так как два угла этого четырехугольника равны 90, то находим выражение для b: b=180-a.
Далее рассмотрим треугольник, образованный двумя r и d. По теореме косинусов находим сначала квадрат d, а потом и само d (в процессе была использована формула приведения: cos(180-a)=-cos(a) )
Конус с углом φ при вершине осевого сечения и радиусом основания r вписан в сферу радиуса R (т. е. вершина конуса лежит на сфере, а основание конуса является сечением сферы, рис. 158, б). Найдите: а) r, если известны R и φ; б) R, если известны r и φ; в) φ, если R = 2r
2.Так как параллелепипед описан вокруг цилиндра, то в основании параллелепипеда лежит квадрат со стороной равной диаметру цилиндра, т.е. . Тогда площадь квадрата (основания) будет равна , а объем
3.Так как по условию призма правильная, то CC1⊥DC и DC⊥AD. Так что по теореме о трех перпендикулярах C1D⊥AD. Далее, в прямоугольном ΔAС1D по теореме Пифагора находим:
Фигура- криволинейный треугольник , ограничен : снизу - прямой у=3, сверху-кривой у=х^3, с боков -прямыми х=корень кубический из 3 и х=2.
Ее площадь = интегралу от f(x)=x^3 в пределах х1=корень куб. из 3 и х2=2. Первообразная=x^4/4 и S=(16-3*корень куб. из 3)/4