У правильній чотирикутній піраміді бічне ребро утворює з висотою кут а (альфа). Відрізок, що сполучає - id1548584020210119 от azmamatovm 19.01.2021 03:32

Question

Геометрия: У правильній чотирикутній піраміді бічне ребро утворює з висотою кут а (альфа). Відрізок, що сполучає основу висоти з серединою бічного ребра, дорівнює a. Знайти об єм піраміди

azmamatovm · Accepted Answer

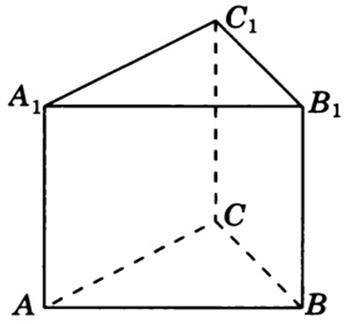
Нехай задана правильна трикутна призма, бічні грані якої є квадратами, а 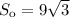$S_{\text{o}} = 9\sqrt{3}$ см² — площа основи цієї призми.

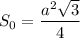
Основа призми є правильним (рівностороннім) трикутником зі строною см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника: $S_{0} = \dfrac{a^{2}\sqrt{3}}{4}$

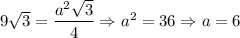Отже, $9\sqrt{3} = \dfrac{a^{2}\sqrt{3}}{4}\Rightarrow a^{2} = 36 \Rightarrow a = 6$ см.

Через те що бічні грані є квадратами, тоді ребра призми дорівнюють 6 см (за властивістю квадрата) — ребра правильної призми є висотою призми.

Об'єм правильної трикутної призми можна розрахувати за формулою

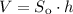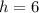$V = S_{\text{o}} \cdot h$ , де h = 6 см — висота призми.

Знайдено значення шуканої величини:

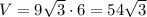$V = 9\sqrt{3} \cdot 6 = 54\sqrt{3}$ см³

Відповідь: А) 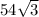$54\sqrt{3}$ см³

MOGZ ответил