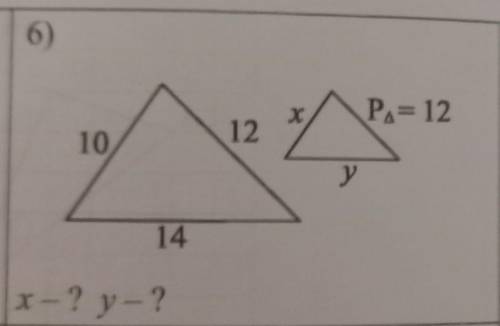
Пусть плоскости α и β параллельны, прямая а перпендикулярна плоскости α. Докажем, что эта прямая перпендикулярна и плоскости β.
В плоскости α проведем две пересекающиеся прямые b и с.
Так как прямая а перпендикулярна плоскости α, то она перпендикулярна каждой из этих прямых.
В плоскости β проведем прямые d║b и е║с.
Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Значит, а ⊥ d и а ⊥ е.
Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна плоскости, ⇒
а ⊥ β.

Объяснение:
Если эти треугольники подобны, то коэффициент подобия равен отношению периметров. Периметр большего треугольника -
10+12+14=36 ед. Периметр меньшего - 12 ед. Их отношение:
36/12=3 - к коэффициент подобия;
х=10/3= 3 1/3 ед;
у=14/3= 4 2/3 ед.