У рівнобедреному трикутнику ABC (AB = BC) точка M перетину медіан віддалена від основи на 4 см. Знайдіть - id1548947420210927 от race201 27.09.2021 02:42

Question

Геометрия: У рівнобедреному трикутнику ABC (AB = BC) точка M перетину медіан віддалена від основи на 4 см. Знайдіть відстань від точки M до вершини B.

race201 · Accepted Answer

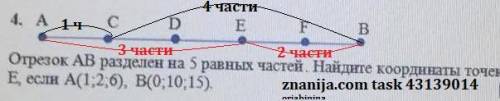
Отрезок АВ разделён на 5 равных частей. Найдите координаты точек С и Е, если А ( 1; 2; 6), В(0; 10; 15) .

Объяснение:

1) Для точки С имеем λ= 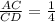$\frac{AC}{CD}=\frac{1}{4}$ =0,25 .

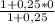x(C)= $\frac{1+0,25*0}{1+0,25}$ =1:1,25=0,8 ,

у(C)= 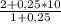$\frac{2+0,25*10}{1+0,25}$ =4,5:1,25=3,6 ,

z(C)= 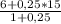$\frac{6+0,25*15}{1+0,25}$ =9,75:1,25=76,8 . Значит С( 0,25 ; 3,6 ; 7,8)

2) Для точки Е имеем λ= 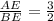$\frac{AE}{BE}=\frac{3}{2}$ =1,5 .

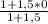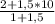x(E)= $\frac{1+1,5*0}{1+1,5}$ =1: 2,5=0,4 , у(E)= $\frac{2+1,5*10}{1+1,5}$ =17 : 2,5=6,8

z(E)= 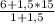$\frac{6+1,5*15}{1+1,5}$ =9,75: 2,5=11,4 Значит С( 0,4 ; 6,8 ; 11,4) .

========================

х=(х₁+λх₂):(1+λ) ,у=( у₁+λу₂):(1+λ) ,где (х₁;у₁), (х₂;у ₂) -координаты концов отрезка , (х;у)-координаты точки, делящей отрезок в заданном отношении.

Отрезок АВ разделён на 5 равных частей. Найдите координаты точек С и Е, если А (1;2;6), В(0;10;15,)

У рівнобедреному трикутнику ABC (AB = BC) точка M перетину медіан віддалена від основи на 4 см. Знайдіть відстань від точки M до вершини B.

MOGZ ответил