
Объем пирамиды вычисляется по формуле
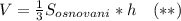
В данном случае площадь основания пирамиды вычислить легко по формуле площади треугольника
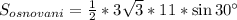
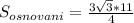
Теперь надо найти высоту пирамиды. Сделать это непросто. Так как нужно узнать: где находится основание высоты пирамиды.
Пусть SO - высота пирамиды. АВС - треугольник в основании пирамиды. Рассмотрим 3 треугольника SOA, SOB, SOC. Все эти треугольники прямоугольные. Так как SO перпендикулярно плоскости основания, а значит перпендикулярно любой прямой в плоскости основания. Далее, SO - общий катет этих прямоугольных треугольников. SA=SB=SC=8 - по условию задачи. Значит эти треугольники равны по катету и гипотенузе. Поэтому другие катеты равны тоже между собой OA=OB=OC. Точка О - является центром описанной окружности. Так как расстояние от точки до любой вершины треугольника АВС одно и то же. Найти радиус описанной окружности можно по разным формулам. Можно воспользоваться следующей формулой
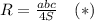
Здесь a, b, и c - стороны треугольника АВС.
Две стороны нам известны. Надо найти третью сторону треугольника АВС.
Найдем ее по теореме косинусов
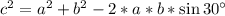
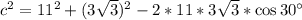
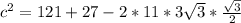

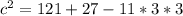
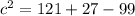
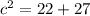
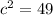
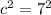
c=7
Значит третья сторона треугольника равна 7.
Подставляем в формулу (*)
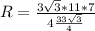
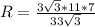
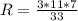
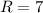
Нашли катет прямоугольного треугольника, образованного высотой пирамиды, боковым ребром и стороной, лежащей в основании пирамиды.
Теперь нам известны гипотенуза прямоугольного треугольника (это боковое ребро пирамиды 8), катет (это радиус описанной окружности треугольника АВС, 7). Осталось найти другой катет (высоту пирамиды). По теореме Пифагора
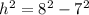
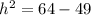
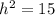
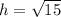
Подставим известные значения в формулу (**)
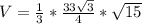
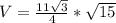
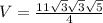
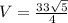
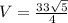
Эта трапеция - "половинка" правильного шестиугольника, вписанного в окружность. Большее основание является диаметром, остальные стороны равны радиусу, диагонали равны 2R(√3/2) = 4√3;
Учитель, конечно же, потребует обоснования единственности такой фигуры - ну, может есть еще какая-то трапеция с такими сторонами, но у неё углы при основании не 60°. На самом деле это все очевидно, но "строго" это так делается - если продолжить боковый стороны до пересечения, то верхнее основание трапеции - средняя линяя получившегося треугольника, поэтому у него все стороны равны...
Еще он потребует объяснить, почему диагонали перпендикулярны боковым сторонам. Ну, с этим вы справитесь :)...