Дано :
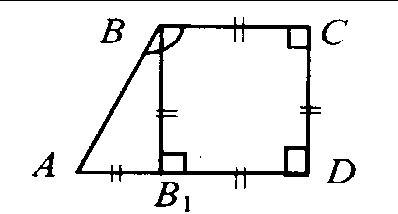
трапеция ABCD ( AD BC )
∠A = ∠B =90° ; °
CH ⊥ AD ;
∠D =45° ;
а) AH =4 м ; DH =1 м ;
или
б) AH =1 м ; DH =4 м.
——————————
AB -? ; BC -? ; CD -? ; AD -?
Решение(Доказательство):
а)
Из прямоугольного треугольника CHD :
CH = DH = 1 м т.к. ∠D =∠DCH =45° ⇒ CD= √(CH²+DH)²=√2 (м) .
AB = CH = 1 м ; BC =AH = 4 м ;AD=AH м. + DH м. =4 м. +1 м. =5 м .
S =((AD +BC)/2 ) * CH =((5+4)/2)* 1 = 4,5 (м² ) .
б)
CH = DH = 4 м т.к. ∠D =∠DCH =45°⇒ CD= CH√2 =4√2 ( м) .
AB = CH = 4 м ; BC =AH = 1 м ;AD=AH + DH =1 м. +4 м. =5 м .
S =((AD +BC)/2 ) * CH =((5+1)/2)* 4 = 12 (м² ) .
https://tex.z-dn.net/?f=%5Ccfrac%7Bsin%5E2a%2B2cos%5E2a-1%7D%7Bctg%5E2a%7D%3Dsin%5E2a
вспоминаем тождественные преобразования:
https://tex.z-dn.net/?f=2cos%5E2a-1%3Dcos2a%3Dcos%5E2a-sin%5E2a значит,
https://tex.z-dn.net/?f=%5Ccfrac%7Bsin%5E2a%2B(cos%5E2a-sin%5E2a)%7D%7Bctg%5E2a%7D%3Dsin%5E2a%5C%20%5Ctextless%20%5C%20%3D%5C%20%5Ctextgreater%20%5C%20%5Ccfrac%7Bcos%5E2a%7D%7Bctg%5E2a%7D%3Dsin%5E2a
вспоминаем, что https://tex.z-dn.net/? f=ctg%5Ena%3D%5Ccfrac%7Bcos%5Ena%7D%7Bsin%5Ena%7D и всё сразу становится на свои места