1.
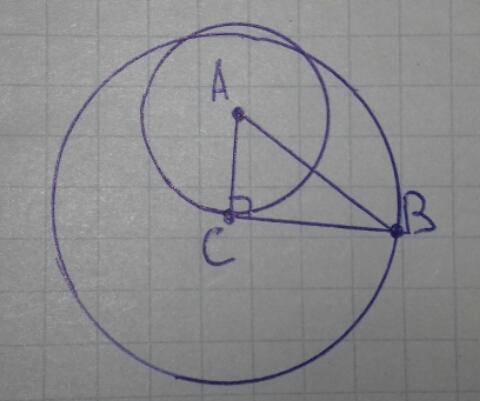
BC⊥AC как катеты прямоугольного треугольника.
BC∩AC = C; AC - радиус окружности с центром A.
Получаем, что BC перпендикулярно радиусу (AC) окружности с центром A и BC пересекает этот радиус в точке (C), принадлежащей той же окружности, поэтому BC это касательная.
2.
AB пересекает окружность (C, CB) в точке B, а CB это радиус той же окружности, проведёный к точке B. Если AB было бы касательной, то AB⊥BC, но это не возможно т.к. AB - гипотенуза, а BC - катет одного прямоугольного ΔABC. Поэтому AB не может быть касательной.
1)так как формула площади основания равна пи*r^2 где знак * умножить а ^ степень
2)пи*r^2=9*пи по условию значит r=3
3)формула объема пи*r^2*h=18*пи значит h=2
4)площадь полной поверхности=2*пи*r*(r+h)=30*пи
ответ 30*пи