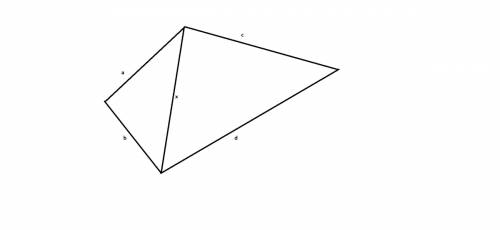
Это верно для произвольного 4 угольника (трапеция частный случай):
Проведем диагональ x.
Запишем неравенство треугольника abx: a+b>x ;
Запишем неравенство треугольника cdx : c+x>d ;
Сложим эти неравенства почленно: a+b+c+x>x+d .
Откуда: a+b+c>d .
Таким образом , любая сторона четырехугольника меньше суммы трех других его сторон , что ,соответственно, справедливо и для трапеции.
Ну наверное самые любознательные спросят :,,А верно ли это для произвольного многоугольника?'' Таки да это так :) . Но вот как это доказать? Пусть эта задача останется вам.Дам небольшую подсказку : примените похожий метод как для 4 угольника ,используя метод математической индукции. Удачи!
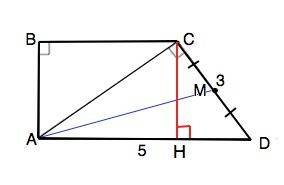
В трапеции ABCD угол A равен 90, градусов, боковая сторона CD перпендикулярна диагонали AC; CD равен 3 см, AD равен 5 см, 1) Найти площадь трапеции. 2) Найти площадь треугольника AMD, если M – середина CD.
1) АВ⊥АD, ВС║AD ⇒ ∠В=90°
СН - высота (ABCD)
Площадь трапеции равна произведению её высоты на полусумму оснований.
S(ABCD)=CH•(BC+AD):2
CH=AC•CD:AD
AC=√(AD²-CD²)=√(5²-3²)=4
CH=3•4:5=2,4 (см)
BC=AH=√(AC²-CH²)=√(16-5,76)=3,2
S(ABCD)=2,4•(3,2+5):2=9,84 см²
* * *
2) Найти площадь треугольника AMD, если M – середина CD.
СМ=MD ⇒АМ - медиана и делит площадь ∆ АСD пополам (свойство).
S AMD=[AC•CD:2]:2=4•3:4=3 см²
1) Треугольник ОВА равнобедренный с катетами 12√2
тогда: ОА=√(288+288)=24
2) Обозначим точки касания В и С тогда треугольник АОВ прямоугольный, найдем катет АВ:
АВ=√(48-36)=2√3
Найдем высоту этого треугольника:
S=0,5AB*OB=0,5*6*2√2=6√2
h=2S/AO=12√2/4√2=3
следовательно хорда ВС=2h=6
Тогда треугольник ОВС равносторонний и угол ВОС=60°
Угол ВАС=360°-180°-60°=120°
3) Так как диагонали ромба точкой пересечения К делятся пополам и взаимно-перпенидкулярны, то радиус окружности проведенный в точку касания К перпендикулярен АС, следовательно АС - касательная.
4) Вершины этого четырехугольника разделили окружность на дуги равные:
х+2х+8х+7х=360°
18х=360°
х=20°
Величины вписанных углов равны половине дуги на которую они опираются следовательно углы четырехугольника равны:
30° , 100°, 150° , 80°
5) Диаметр окружности равен 50, следовательно радиус равен 25