Объяснение:
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны
Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
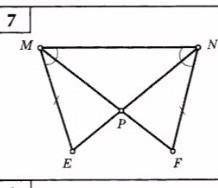
ВОТ ПРАВИЛА : САМА ДУМАЙ АХАХ НО Я ХЗ Я ДУМАЮ ЭТО 1 ПРИЗНАК Х
Объяснение:
а)Основанием пирамиды служит квадрат, проекцией бокового ребра в √17 см, есть половина диагонали основания, которая равна а√2=4√2, а ее половина 2√2 см, тогда высота пирамиды может быть найдена как √((√17)²-(2√2)²)=√(17-8)=√9=3/см/
б)Площадь полной поверхности состоит из площади боковой поверхности и площади основания. Площадь основания равна 4²=16/см²/, а площадь боковой поверхности - это сумма четырех площадей треугольников со сторонами √17см; √17см и 4см. ЕСли провести из вершины пирамиды высоту на сторону основания, то можно найти эту апофему. Она равна √((√17)²-(4/2)²)=√(17-4)=
√13, умножая теперь апофему ( это высота боковой грани правильной пирамиды) на основание, равное 4, деля на два и умножая на 4, получим площадь четырех равных треугольников,т.е. площадь боковой поверхности.
4*(4*√13 )/2= 8√13/см²/, а площадь полной поверхности равна
16+8√13 =8*(2+√13) / см²/
Подробнее - на -
8√3/(1+√3) см
Объяснение:
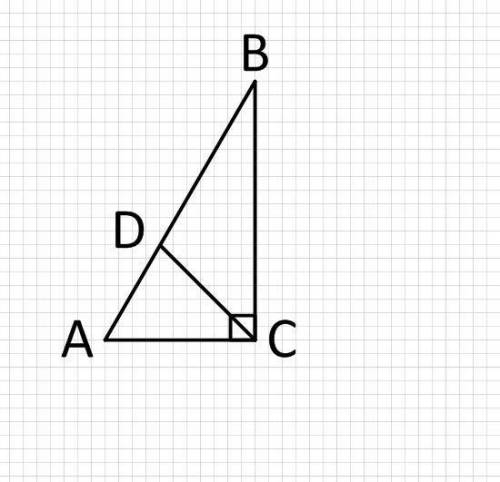
По свойству прямоугольных треугольников, катет лежащий напротив угла в 30 градусов равен половине гипотенузы
AC=AB/2=8/2=4 см
По теореме Пифагора найдет третью сторону прямоугольного треугольника ACB:
AB²=AC²+BC²
BC²=AB²-AC²
BC=√(AB²-AC²)=√(64-16)=√48 =4√3 см
Биссектриса делит противоположную сторону треугольника пропорционально прилегающим сторонам:
AD/BD = AC/BC
учитывая, что
AD=AB-BD
получаем:
(AB-BD)/BD = AC/BC
AB/BD-BD/BD=AC/BC
AB/BD-1=AC/BC
AB/BD=AC/BC+1
BD=AB:(AC/BC+1)
BD=8:(4/(4√3)+1)=8:1/√3+8=8√3/(1+√3) см
По стороне и двум прилежащим к ней углам.