Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
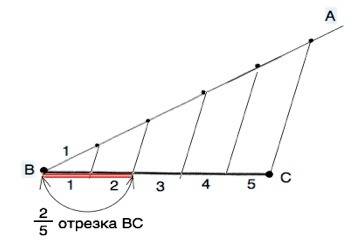
Пусть дан отрезок ВС.
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
найдем через теорему косинусов. a^2=b^2+c^2-abc cos(A), b^2=a^2+c^2 - 2ac cos(B)
b^2=144 + 225 - 2*12*15 * cos 40, b^2=369 - 360 * (AB/BC)= 369 - 360 * (12/15)= 369 - 288 = 81 => b = корень из(81) = 9