Отрезки MF и DK пересекаются в середине О отрезка MF, Угол ОМD = углу OFK.
Докажите, что треугольник DMO=треугольнику KFO

Question

Геометрия: Отрезки MF и DK пересекаются в середине О отрезка MF, Угол ОМD = углу OFK. Докажите, что треугольник DMO=треугольнику KFO

rassslabon · Accepted Answer

Найдём гипотенузу АВ по теореме Пифагора - АВ² = АС² + ВС² = 8² + 6² = 64 + 36 = 100 ⇒ АС = √АС² = √100 = 10 см.

Синус острого угла прямоугольного треугольника - это отношение противолежащего катета к гипотенузе.Косинус острого угла прямоугольного треугольника - это отношение прилежащего катета к гипотенузе.Тангенс острого угла прямоугольного треугольника - это отношение противолежащего катета к прилежащему катету.Котангенс острого угла прямоугольного треугольника - это отношение прилежащего катета к противолежащему катету.

Отсюда -

$sin\angle A = \frac{CB}{AB} = \frac{6}{10} = \frac{3}{5} .$

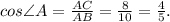
$cos\angle A = \frac{AC}{AB} = \frac{8}{10} = \frac{4}{5} .$

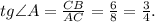
$tg\angle A = \frac{CB}{AC} = \frac{6}{8} = \frac{3}{4} .$

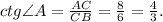
$ctg\angle A = \frac{AC}{CB} = \frac{8}{6} = \frac{4}{3} .$

Отрезки MF и DK пересекаются в середине О отрезка MF, Угол ОМD = углу OFK. Докажите, что треугольник DMO=треугольнику KFO

MOGZ ответил

Отрезки MF и DK пересекаются в середине О отрезка MF, Угол ОМD = углу OFK.
Докажите, что треугольник DMO=треугольнику KFO