2)в треугольнике abc точка k принадлежит стороне ab,а точка p стороне ac.отрезок kp || bc.найдите периметр - id155492120201110 от newsergy81 10.11.2020 14:01

Question

Геометрия: 2)в треугольнике abc точка k принадлежит стороне ab,а точка p стороне ac.отрезок kp || bc.найдите периметр треугольника akp,если ab=12см,bc=10см ,ac=16см ,ak=6см умных людей с напишите решение

newsergy81 · Accepted Answer

1) Пусть касается нужная касательная в точке К. Расстоянием от АВ до К будет расстояние от середины отрезка АВ до точки К. Так как треугольник АОВ - равнобедренный, то высота, биссектриса и медиана будет одним и тем же отрезком. Пусть АМ=МВ. Значит МК=МО+ОК нам нужно найти. ОК - уже известно, так как это радиус. Осталось найти МО. МО - можно найти по теореме Пифагора. МВ - половина АВ, значит МВ=12 см.

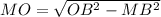
$MO=\sqrt{OB^2-MB^2}$

$MO=\sqrt{13^2-12^2}$

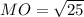
$MO=\sqrt{25}$

MO=5 см.

Значит МК=МО+ОК

МК=5+13

МК=18.

ответ: расстояние равно 18 см.

2) Ведь у четырехугольника ACBO два угла прямые: это угол CAO и угол CBO, так как они являются касательными к окружности. В четырехугольнике всего 360 градусов. Значит AOB=360-90-90-50=130 градусов.

ответ: 130 градусов

MOGZ ответил