
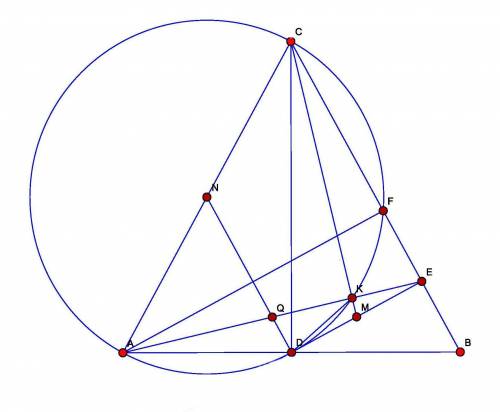
Вместо того, чтобы проводить отрезок CM (см. чертеж), я построил окружность на AC, как на диаметре. Середина AC - точка N - это центр этой окружности. Эта окружность проходит через все точки, из которых AC видна под прямым уголом, в частности - через точки D и F (основание высоты, в решении не нужна :) ).
Отрезок DE из условия является касательной к это окружности в точке D, так как ND II CB, как средняя линия треугольника ABC, то есть DE перпендикулярно радиусу ND.
В том числе эта окружность пересекает AE в точке K (из неё AC тоже видна под прямым углом, то есть ∠CKA = 90°). Я провожу отрезки CK и KM (M - середина DE), не предполагая, что они лежат на одной прямой. Для того, чтобы это "случилось", необходимо, чтобы ∠EKM = 90°. Вот это я и буду доказывать.
Треугольники AED и DKE подобны по 2 углам (один угол общий, а ∠KAD = ∠KDE, поскольку один угол вписаный, а другой лежит между касательной и секущей, и оба измеряются половиной дуги DK.
ND делит отрезок AE пополам (как средняя линия тр-ка ABC, ND делит пополам любую чевиану из вершины A), то есть Q - середина AE. Точки Q и M являются соответственными точками двух подобных треугольников, поэтому ∠QDE = ∠MKE = 90° чтд.
Если слова "являются соответственными точками" не понятны, то можно и так сказать - треугольники QDE и MKE подобны по двум пропорциональным сторонам и общему углу: QE и ME являются половинами сторон подобных треугольников AED и DKE, поэтому QE/ME = AE/ED = ED/EK;
Даны вершины треугольника А(-1;2;3), В(3;-2;1), С(2;1;-1).
Точка М = (А(-1;2;3) + В(3;-2;1)) / 2 = (1; 0; 2).
Вектор CМ = (1-(-1); 0-2; 2-3) = (2; -2; -1).
Длина CМ = √(4 + 4 + 1) = √9 = 3.
Длины сторон находим как расстояние между точками.
d = √((х2 - х1 )² + (у2 - у1 )² + (z2 – z1 )²)
АВ ВС АС Р р=Р/2
6 3,741657 5,099019 14,8406 7,4203.
36 14 26 квадраты.
Как видим, треугольник РАЗНОСТОРОННИЙ.
Находим косинус угла между ВА и ВС.
Вектор ВА -4 4 2, модуль равен 6.
Вектор ВС -1 3 -2, модуль равен √14.
cos B = (-4*(-1) + 4*3 + 2*(-2)) / (6*√14) = 12 / 22,44994432 =
= 0,534522484.
Радианы 1,006853685
Угол В = градус 57,68846676.