Объяснение:
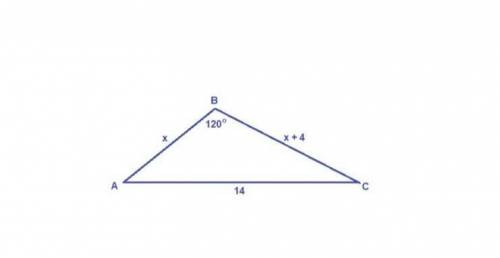
представим треугольник в виде ABC
где
AB=x
BC=x+4
используем теорему косинусов (по другому никак)
Т. косинусов гласит:
AC²=AB²+BC² - 2AB*BC* cos<ABC
подставляем все что нам известно:
14²=x²+(x+4)²- 2x(x+4)*(-1/2)
196=2x²+8x+16+x²+4x
3x²+12x-180=0 / :3 (- разделем на 3)
x²+4x-60=0
решу по т.в, но можешь через дискриминант:
x= 6
x= -10 (сторона "-10" быть не может, это не подходит)
=> AB=6 и подставляем, чтобы найти другую сторону:
BC= x+4 = 6+4 = 10
Найдем площадь:
Используем теорему Герона (больше никак нельзя):
Найдем полупериметр:
p= (6+10+14)/2 = 15 cm
дальше используем т.Герона:
S= 15/√(15(15-14)*(15-6)*(15-10))
- тут знаменатель это весь корень
S= 15/√(15*1*9*5) = √675 = 15√3
Объяснение:
а) Сперва доказываем что тр. АВС подобен тр. MNK по 1 признаку ( 2 угла равны)
Используя свойства подобных треугольников (стороны 1 тр. пропорциональны сторонам 2 тр. И имеют коэффициент k), находим сначала коэффициент k по известным нам сторонам BC и NK, а потом через коэффициент подобия (k) находим остальные стороны по пропорции, и в конце просто складываем.
b) Опять же сперва доказываем что тр. ABC подобен тр. MNK по первому признаку, и снова пользуясь свойством подобных треугольников, выражаем что : Pтр.ABC/Pтр.MNK = k ( коэффициенту подобия).
Находим k по известным нам сторонам, потом находим периметр тр. АВС, подставляем в формулу и просто решаем пропорцию. Надеюсь я