Пусть SABCD - правильная 4-х угольная пирамида.О- точка пересечения диагоналей основания. Тогда SO-высота пирамиды.
Sпов.=Sосн.+Sбок.
Sосн.=а²=6²=36(ед.кв.)
Sбок.=½рl, где р - периметр основания, l-апофема(высота боковой грани).
Росн.=4а= 4·6=24 ед. -поскольку в основании квадрат.
Найдем апофему пирамиды, для этого проведем высоту боковой грани SAB, которая является равнобедренным треугольником. Получим SМ, т.М - середина стороны АВ основания пирамиды, т.к. для треугольника SAB SМ есть высотой, бисектрисой и медианой.
Кроме того по т. о 3-х перпендикулярах ОМ - проекция SМ на основание и ОМ тоже перпендикулярен АВ. Таким образом ОМ - радиус окружности вписаной в основание пирамиды. Для квадрата R=½а=½·6=3.
Из треугольника SОМ(угол О - прямой) по т.Пифагора SМ²=ОМ²+SО², SМ²=3²+4²=9+16=25,
SМ=5.
Sбок.=½·24·5=60(ед.кв.)
Sпов.=60+36=96(ед.кв.)
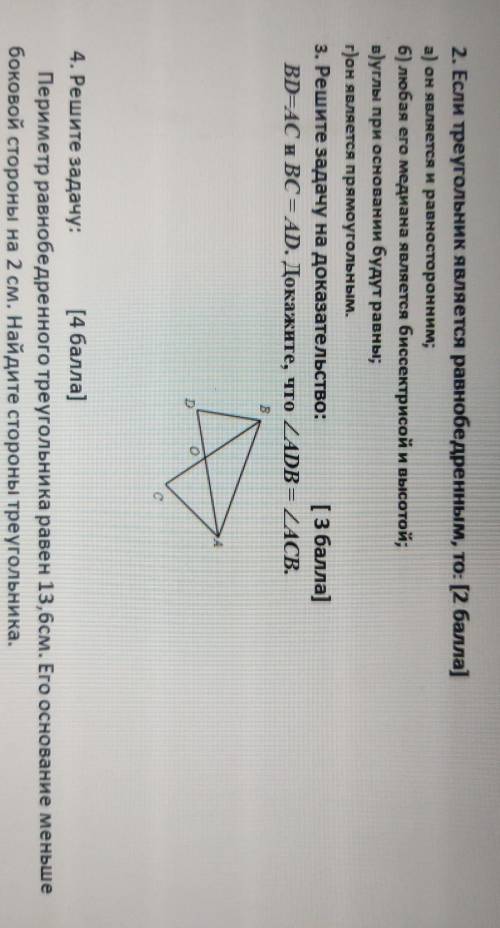
3. BD=AC и BC=AD по условию, АВ общая, следовательно треугольники равны по 3 признаку равенства треугольников, следовательно все его углы равны. (угол ADB равно угол ACB)
Объяснение:
4. боковую сторону возьмем за х, в равнобедренном треугольнике боковые стороны равны, следовательно х*2, основание на 2 см меньше боковой, следовательно х-2, периметр - 13,6. получаем уравнение:
2х+х-2=13,6
3х=15,6
х=5,2
5,2 - боковая
5,2-2=3,2 - основание