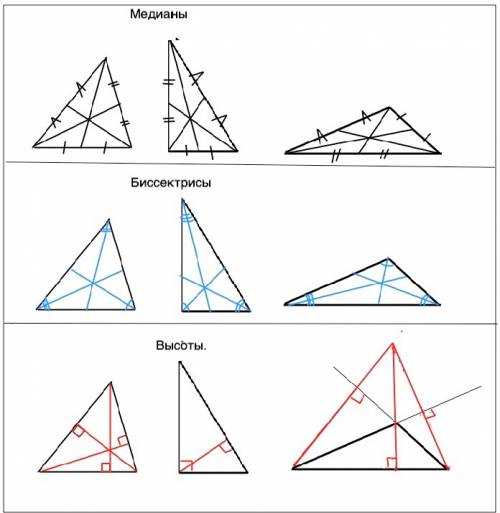
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
Биссектрисы треугольника пересекаются в одной точке, расстояние от которой до сторон треугольника одинаково и является центром вписанной окружности.
Высоты треугольника пересекаются в одной точке. Точка пересечения высот остроугольного треугольника находится внутри него. Точка пересечения высот прямоугольного треугольника - вершина прямого угла.
Высоты тупоугольного треугольника, проведенные из вершин его острых углов, проходят вне его и пересекают продолжения сторон. Точка пересечения высот тупоугольного треугольника находится вне треугольника.
∠АВС = 80°.
Объяснение:
Пусть в равнобедренном треугольнике АВС (АВ = АС) угол
∠А = α.
В равнобедренном треугольнике ADF (AD = DF)
∠DAF = ∠DFA = α.
Внешний угол EDF равен сумме двух внутренних, не смежных с ним, углов: ∠EDF = 2α.
В равнобедренном треугольнике DFЕ (EF = DF)
∠EDF = ∠DEF = 2α.
Угол DFE = 180° - 4α (по сумме внутренних углов треугольника).
Углы DFA, DFE и EFС составляют развернутый угол и значит
DFA + DFE + EFС = 180°.
∠EFC = 180° - (180° - 4α) - α = 3α.
В равнобедренном треугольнике FЕС (EF = ЕС)
∠EFС = ∠EСF = 3α.
Угол FEС = 180° - 6α (по сумме внутренних углов треугольника).
Углы DЕF, FEC и BEC составляют развернутый угол и значит
∠ВЕС = 180° - 2α - (180° - 6α) = 4α.
В равнобедренном треугольнике АВС (АВ = АС)
∠ВЕС = ∠В = 4α.
∠А + 2∠В = 180° (сумма внутренних углов треугольника). => α + 8α = 180° => α = 20°. =>
∠В = 80°.