Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.
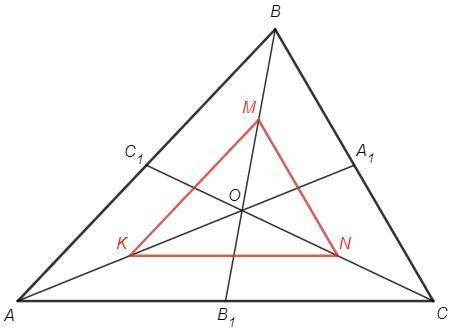
Отрезки KM, MN, KN являются средними линиями в треугольниках AOB, BOC, AOC.
a) KM||AB, MN||BC, KN||AC
KMN~ABC по трем параллельным сторонам
б) KM=AB/2, MN=BC/2, KN=AC/2
P(ABC) =2P(KMN) =44*2 =88 (см)
в) Отношение соответствующих отрезков (медиан, биссектрис, высот и любых отрезков, построенных сходным образом) в подобных треугольниках равно коэффициенту подобия.
k=AB/KM =2
Медианы ABC вдвое больше медиан KMN.
Тогда решим систему уравнений:
1)
{х+у=11
{х^2+у^2=61
2)
{х^2+2*х*у+у^2=121
{х^2+у^2=61
3)
{-х^2-2*х*у-у^2=-121
{х^2+у^2=61
4)
{-2*х*у=-60
{х+у=11
5)
{х*у=30
{х+у=11
6)
{х=11-у
{(11-у)*у=30
•Рассмотрим отдельно вот это уравнение:
(11-у)*у=30
-у^2+11у-30=0
D=121-4*(-1)*30=441
y1=(-11+21)/2=5
y2=(-11-21)/2=-16
Второй корень не подходит по смыслу задачи (катет не может быть отрецателен).
Значит, вернёмся к системе:
7)
{у=5
{х=6
Итак, катеты найдены, теперь по формуле площади прямоугольного треугольника:
S=1/2*a*b, где a и b - его катеты.
S=1/2*5*6=15 см^2.
ответ: 15 см^2.