Объяснение:
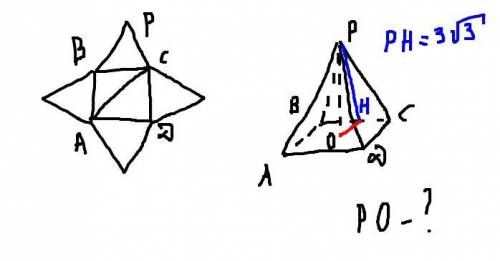
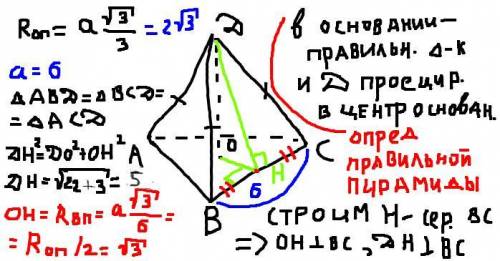
5. Нарисуем пирамиду, назовем центр основания O.
Нужно найти отрезок PO. Для этого нужно найти треугольник, из которого можно посчитать PO по теореме Пифагора( то есть прямоугольный треугольник, в котором участвует PO). Раз такого треугольника не видим явно из условия, придется его построить, при этом нужно задействовать известные данные. Нам известна диагональ квадрата, значит, можно посчитать его сторону, также известна длина отрезка PH.
Поэтому построим треугольник POH, проведем OH. Треугольник POH будет прямоугольным, потому что PO - отрезок, соединяющий вершину правильной пирамиды с центром ее основания, а такой отрезок перпендикулярен основанию пирамиды. Тогда в ΔPOH угол ∠POH - прямой.
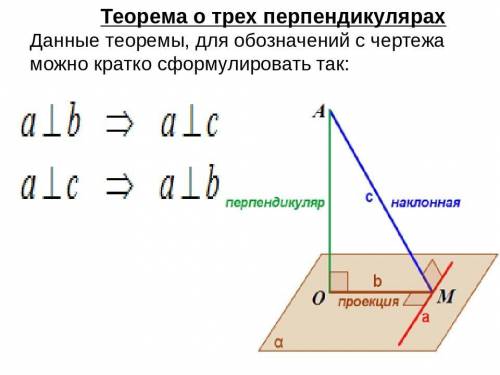
Осталось найти OH. Так как PO перпендикулярно плоскости основания, а PH перпендикулярно BC, то по следствию из теоремы о трех перпендикулярах OH будет перпендикулярно BC.
H - середина BC(PH - высота равнобедренного треугольника, значит, PH также и медиана, а Δ-к равнобедренный, потому что пирамида правильная ), поэтому CH в 2 раза меньше BC. Прямоугольные треугольники OHC и ABC подобны по двум углам, поэтому OH также в 2 раза меньше AB.
AB - сторона квадрата ABCD, а сторона квадрата в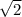 
меньше его диагонали. Тогда AB = 12/
Теперь находим OP по теореме Пифагора
OP = 
= 
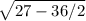= 3 см
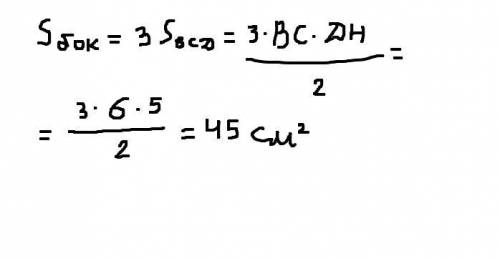
ответ: 15,777π, иначе 49,54 (ед. площади)
Объяснение: Формула площади круга S(кр)=πr^2
Нужный радиус можно найти по одной из формул площади треугольника:
S = r•р, где р — полупериметр, r — радиус вписанной окружности⇒
r=S/p
По другой формуле Ѕ ∆ MKN=MK•NK•sin30°/2.
Ѕ=20•20•0,5/2=100 (ед.площади).
Для нахождения периметра третью сторону найдем по той же формуле, но с другой стороной:
Ѕ(MKN)=МК•МN•sin(KMN)/2
∆MKN - равнобедренный, ⇒углы при МN=(180°-30°)/2=75°
sin75°≈0,9659
100=20•MN•0,9659/2⇒
MN≈10,353
p(MKN)=0,5•(2•20+10,353)≈25,1765
r=S/p=100/25,1765≈3,972
Ѕ(круга)=πr²=15,777π или при π=3,14 S(круга)=49,54 (ед. площади)
В прямоугольном ΔАВС, ∠С=90° , АВ=25 см ,АС=24 см . Найти катет а, острые углы α,β. Решите задачу двумя
Объяснение:Чертеж к данной задаче не нужен. Решается аналитическим
По т. Пифагора СВ=√(25²-24²)=√( 25-24)(25+24)=7 (см) .
∠A=α , sinα=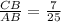
=0,28 ⇒ α=16° ,
∠B=β , cosβ=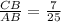
=0,28 ⇒ β=74° .
∠A=α , cosα=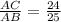
=0,96 ⇒ α=16° ,
∠B=β=90°-16°=74° ,
cosβ=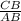
,0,28=
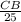⇒ CB=0,28*25 =7 (см) .