MN- будет совпадать с диаметром тогда и только тогда, когда описанная трапеция - квадрат. В противном случае диаметр лежит на этой средней линии, т.к. она проходит через центр окружности и диаметр будет меньше этой средней линии. То, что диаметр принадлежит средней линии вытекает из того, что отрезок соединяющий середины оснований трапеции - перпендикулярен основаниям ,проходит через центр окружности равен двум радиусам и делится центром окружности пополам ( т.е. этот отрезок, как раз совпадает с диаметром). А средняя линия тоже делит этот отрезок пополам значит тоже проходит чрез центр окружности.
Найдём координаты точки С - середину отрезка ВМ: С((2-4)/2=-1; (3-3)/2=0; (1-1)/2=0) = (-1; 0; 0). Расстояние от точек В и М до С равно: ВС= МС = √((-1-2)²+(0-3)²+(0-1)²) = √(9+9+1) = √19.
Если в эту систему координат поместить сферу с центром в точку С, то любая точка на сфере составляет с точками В и М прямой угол.
Уравнение сферы: (x-xo)²+(y-yo)²+(z-zo)² = R². На оси OZ координаты по х и по у равны нулю. Подставим нули в уравнение сферы с центром в точке С и радиусом √19: (0-(-1))²+(0-0)²+(z-0)² = 19. 1+z² = 19. z² = 18. z = +-√18 ≈ +-4,24264. ответ: координаты точек А и А1 на оси ОZ равны +4,24264 и -4,24264.
11.
Дано:
ΔАВС - равнобедренный
АС = ВС = 13
АВ = 10
Найти:
АС - высоту. опущенную на боковую сторону
СD - высота равнобедренного треугольника. опущенная на основание, является и медианой. Поэтому AD = BD = 0.5AB = 0.5 · 10 = 5.
По теореме Пифагора
АС² = CD² + AD²
13² = CD² + 5²
CD² = 13² - 5² = 144 = 12²
CD = 12
Площадь треугольника АВС
S = 0.5 CD · AB = 0.5 · 12 · 10 = 60
Площадь треугольника АВС можно также вычислить и так:
S = 0.5 BC · AE
откуда
АЕ = 2S : BC = 2 · 60 : 13 = 9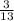 ≈ 9.23
≈ 9.23
АЕ = 9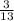 ≈ 9.23
≈ 9.23
12.
Дано:
MKNR - ромб
KR = 10 - 1-я диагональ ромба
MN = 12 - 2-я диагональ ромба
Найти:
МК - сторону ромба
Пусть О - точка пересечения диагоналей ромба.
Диагонали ромба делятся точкой пересечения пополам, поэтому
КО = 0,5 KR = 0.5 · 10 = 5
МО = 0,5 MN = 0.5 · 12 = 6
Диагонали ромба пересекаются под прямым углом, поэтому
КО ⊥ МО и ΔМКО - прямоугольный с гипотенузой МК.
По теореме Пифагора
МК² = КО² + МО²
МК² = 5² + 6² = 61
МК = √61 ≈ 7,81
Сторона ромба МК =√61 ≈ 7,81