в четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны.
трапеция - четырехугольник, следовательно, если в неё можно вписать окружность, то сумма ее оснований равна сумме боковых сторон.
сумма оснований данной трапеции 3+5=8, а её средняя линия равна 4
пусть длина меньшего основания а . тогда длина большего - 8-а.
средняя линия трапеции делит саму трапецию на две меньшего размера, высоты каждой из которых равны половине высоты исходной.
площадь трапеции равна полусумме оснований, умноженной на высоту.
пусть высота каждой части трапеции равна h.
тогда площадь верхней трапеции будет (а+4)•h: 2,
а площадь большей (8-а+4)•h: 2=(12-а)•h: 2
по условию отношение этих площадей равно 5/11⇒
[ (а+4)•h: 2]: [ (12-а)•h: 2]=5/11
отсюда 60-5а=11а+44
16а=16
а=1
подробнее - на -
Знайдемо радіус основи:
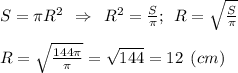
Діаметр d (AB) = 2R = 2*12 = 24 (см)
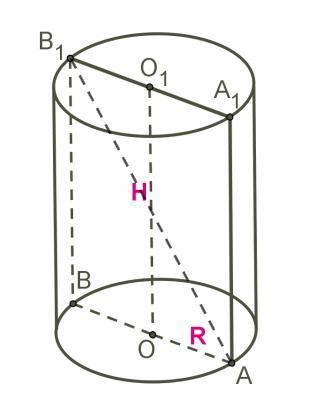
Осовий переріз — це прямокутник (AA₁B₁B), перпендикулярний основі, який проходить через центральну вісь циліндра. AB₁ - діагональ, яка ділить осьовий переріз на два конгруентні прямокутні трикутники, і являється гіпотенузою.
Розглянемо ΔAB₁B:
∠B = 90° ⇒ ΔAB₁B — прямокутний. AB₁ = 25 см, АВ = 24 см. Знайдемо невідомого довжину катета B₁B.
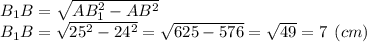
Будь-яка твірна циліндра є його висотою: BB = h = 7 (см)
Розглянемо прямокутник AA₁B₁B:
AA₁B₁B — це осьовий переріз, який являє собою прямокутник з шириною AB = 24 см та висотою B₁B = 7 см. Знайдемо площу:
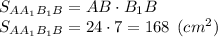
Відповідь: довжина твірної циліндра рівна 7 см, площа осьового перерізу циліндра рівна 168 см².
Задача решается проще, если вспомнить, что медианы в точке пересечения (т. е. все три медианы в любом треугольнике пересекаются внутри него строго в одной точке - это центр тяжести треугольника). Так вот эти медианы делятся в точке пересечения в соотношении 2 к 1, считая от вершины. Значит ВО=15*2/3=30/3=10 см, СО=18*2/3=6*2=12 см.
ОВ1=15/3=5 см, ОС1=18/3=6 см. Теперь нужно вспомнить теорему Пифагора. Треугольник ВОС - прямоугольный, значит ВС - гипотенуза.
Треугольник ВОС1 - тоже прямоугольный, так как угол С1OB - прямой. Доказывается так.
По теореме Пифагора из треугольника находим гипотенузу ВС1.
Заметим, что BC1 - половина АВ по определению медианы СС1.
Треугольник B1OC - прямоугольный, так как угол B1OC - прямой, как вертикальный к углу С1OB. Та же теорема Пифагора, чтобы вычислить гипотенузу В1С.
B1C=13 см.
Заметим также, что В1С - половина АС. Значит АС=26 см.
Вычислим периметр АВ.