
Объяснение:
{ AM - MB = 7
{ MB = AM\2
=>
AM - (AM\2) = 7 > 2AM - AM = 14 >
AM = 7 и
MB = AM\2 = 7\2 = 3,5
11) AM =MB = AB > L A = L M = L B = 180\3 = 60 град.
AM = MB и MD _|_ AB > L AMD = L M\2 = 60\2 = 30 град. =>
DM = 2 * DE = 2 * 4 = 8
14) AKM = AEM, так как L MAK = L MAE и L AKM = L AEM =>
и L AMK = L AME => треугольники подобны по трем углам, а равны, так как гипотенуза АМ общая =>
KM = EM = 13
15) L CMB = 180 - (L C + L CBM) = 180 - (70 + 40) = 70 град.
L BMD = 180 - (L MBD + L MDB) = 180 - (40 + 90) = 50 град.
L AMD = 180 - (L CMB + L BMD) = 180 - (70 + 50) = 60 град. =>
MD = AM\2 = 14\2 = 7 Незнаю наверное правильно
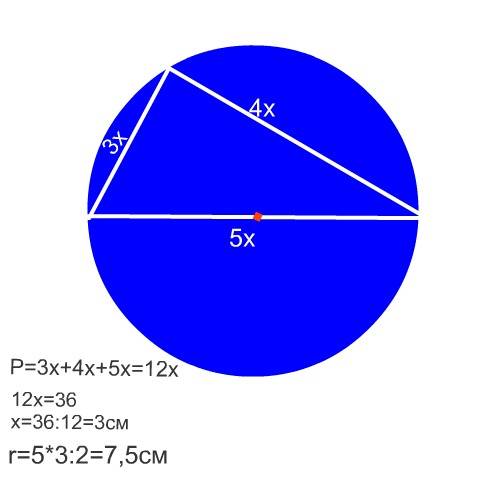
Гипотенуза этого прямоугольного треугольника является диаметром окружности.
Так как отношение катетов 3:4, то гипотенуза в этом отношении будет 5,
т.е все стороны треугольника относятся как 3:4:5, поскольку этот треугольник - египетский.
Примем коэффициент отношения сторон за х
тогда его периметр равен
3х+4х+5х=12х
Коэффициент равен 36:12=3
Диаметр круга
3*5=15 см
Радиус 15:2=7,5 см
-------------------------------
Боковую сторону можно найти через синус угла при вершине треугольника.
Он равен 180-2а
х=h: sin(180-2а)
AC=√AB^2+BC^2-2*AB*BC*cos(120)=4+49+14=67 за теоремой косинусов
BD=√BC^2+CD^2-2*BC*CD*cos(60)=4+49-14=39
Объяснение: