Дано: Треугольник АВС. АВ=ВСб М∈BD, K∈AC. MK║AB. <ABC=126°,<BAC=27°.
Найти <MKD, <KMD и <MDK.
Решение.
Треугольник АВС равнобедренный, следовательно BD - биссектриса, высота и медиана треугольника. <BAC=<BCA=27°, Значит
<ABD = (1/2)*(<ABC) = 126/2 = 63°. <BDA=<MDK = 90°.
MK параллельна АВ, значит <MKD=<BAC=27°, а <KMD=<ABD=63°, как соответственные углы при параллельных прямых АВ и МК и секущих AD и BD соответственно.
ответ: <MKD=27°, <KMD=63°, <MDK=90°.

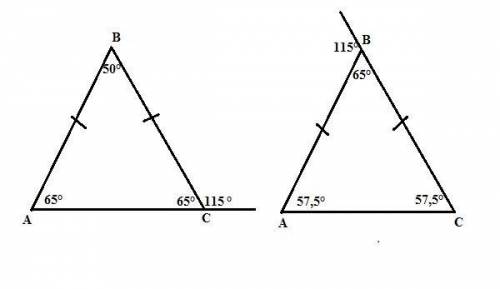
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
ответ: 30°, 30°, 120°, 16, 16, 16√3.
Объяснение:
Теореме синусов:
a/sinA=b/sinB=c/sinC. sin30°=1/2. c=16.
c/sinC=B/sinB;
16/1/2=b/1/2;
b=16.
∠C=180°-(30°+30°)=180°-60°=120°. Sin 120°=√3/2=0.866;
a/sinA=c/sinC; a= c*sinC/sinA=16*√3/2:1/2=16√3.
***
∠А=∠В=30° - треугольник АВС - равнобедренный.
AB=AC=16.
Высота ВЕ=16/2=8. (катет против угла в 30°).
Сторона АС=2*√16²-8²=2*√256-64=2√192=2*8√3=16√3.