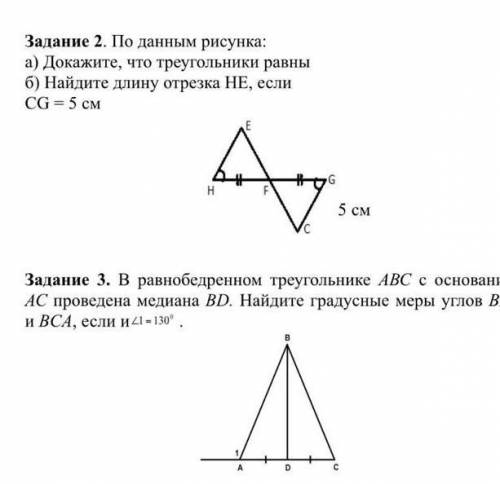
3,5 м
Объяснение:
*Рисунок прикреплен*
1) Стена перпендикулярна полу, => треугольникАВС - прямоугольный
По теореме Пифагора найдем расстояние от пола до верхнего конца лестницы :
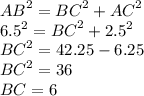
2) Лестница отодвинута от стены еще на 3,5 метра. Образуется новый треугольник А1B1C .Он также прямоугольный . Рассмотрим его стороны :
А1В1= 6,5 м (т.к. это лестница) ;
А1С= 2,5+3,5= 6 м
3) По теореме Пифагора найдем расстояние от пола до верхнего конца лестницы :
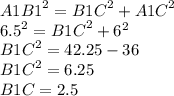
4) Чтобы найти расстояние, на которое лестница опустилась по стене (т.е. длину отрезка ВВ1 ) , вычтем В1С из ВС :
ВС- В1С= 6- 2,5= 3,5 м
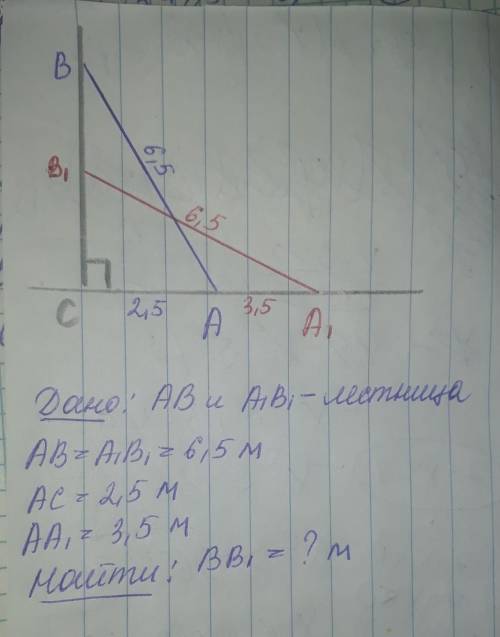
В правильной треугольной пирамиде сторона основания равна a, а боковое ребро – b. Через сторону основания пирамиды под углом α к основанию проведена плоскость β, которая пересекает пирамиду. 1. Изобразите сечение пирамиды плоскостью β. 2. Обоснуйте положение угла α. 3. Найдите площадь сечения. 4. Сделайте анализ ответа относительно параметров задачи.
Объяснение:
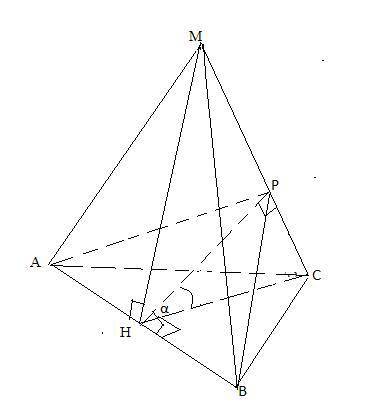
АВСМ-правильная пирамида.
Пусть МН⊥АВ, тогда СН⊥АВ( как проекция наклонной МН) по т. о тре перпендикулярах. Тогда АВ ⊥МН и АВ⊥СН ⇒ АВ⊥(МНС) по признаку перпендикулярности прямой и плоскости. Проведем в плоскости (МНС) отрезок НР⊥МС. Отрезок НР ⊥АВ и СН⊥АВ ,как лежащие в плоскости (МНС). Значит ∠РНС-линейный угол двугранного угла между плоскостями β (АВР) и ( АВС).
В сечении пирамиды плоскостью β получился ΔАВР -равнобедренный
° ΔАРН=ΔВРН как прямоугольные (РН⊥АВ), по 2-м катетам АН=НВ, НР-общий;
° Соответственные элементы в данных треугольниках равны ⇒АР=ВР.
S(ABP)=0,5*АВ*РН.
ΔВ НС , НС=а√3/2 по т. Пифагора.
Найдем РН из ΔРНС-прямоугольного сosα=HP/HC или сosα=HP/(а√3/2) или НР=(а√3*сosα)/2
S(ABP)=0,5*а*(а√3*сosα)/2
S(ABP)= 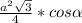 .
.
4. Сделайте анализ ответа относительно параметров задачи. может лишнее условие (b)
ответ:Удачи сделать
Объяснение:СОР