с Геометрией у нас Сор 10 класс Отрезки FО, NО и CО попарно перпендикулярны между собой. Найти периметр и косинус угла CNF треугольника NFC, если CО = ОF = 5 см, ОN = 12 см.

👇

Увидеть ответ

Ответ:

gulkogulkovno

07.02.2023

Думаю что в этом году в Москве будет

4,6(95 оценок)

Открыть все ответы

Ответ:

aidaXD

07.02.2023

Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла.
Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке.
Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей.
Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов.
Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов.
Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48.
Можно было бы и далее продолжать таким но мы замечаем закономерность.
Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле: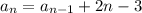
$a_n = a_{n-1} +2n -3$ , где n - число лучей кратное 3.
Пробуем вычислить по этой формуле:

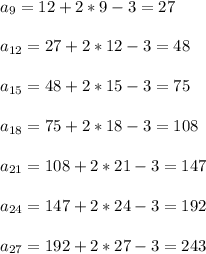
$a_{9} = 12 + 2*9 - 3 =27 \\ \\ a_{12} = 27 + 2*12 - 3 =48 \\ \\ a_{15} =
48 + 2*15 - 3 =75 \\ \\ a_{18} = 75 + 2*18 - 3 =108 \\ \\ a_{21} = 108 + 2*21 -
3 =147 \\ \\ a_{24} = 147 + 2*24 - 3 =192 \\ \\ a_{27} = 192 + 2*27 - 3
=243$

Итак, ответ найден. Для 27 лучей возможно максимум 243 тупых угла.
Так считать долго, можно увидеть формулу для прямого расчёта: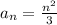

$a_n = \frac{n^2}{3}$
По этой формуле можно считать для любого количества лучей, кратное трём.

4,4(49 оценок)

Ответ:

ляляляляляляля1

07.02.2023

1. 4√7 см

Дивись на фото.

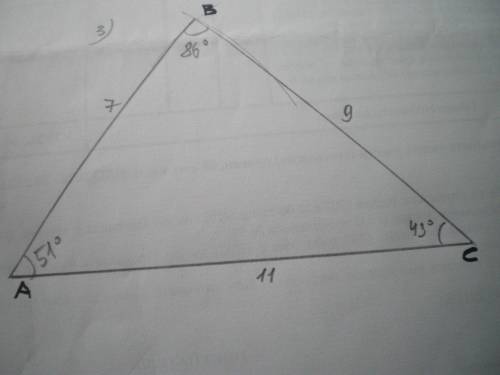
За теоремою косинусів АС²=АВ²+ВС²-2*АВ*ВС*сos∠В.

121=49+81-2*7*9*cos∠В

126 cos∠В = 9; cos∠В=0,07143; ∠В≈86°

ВС²=АВ²+АС²-2*АВ*АС*cos∠А

81=49+121-2*7*11*cos∠А

144 cos∠А=89

cos∠А=0,61805; ∠А≈51°

∠С≈180-(86+51)≈43°

Дано: КМРТ паралелограм, КР=26 см, МТ=18 см, КТ=х см, КМ=х-10 см.

Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін.

Див на фото:

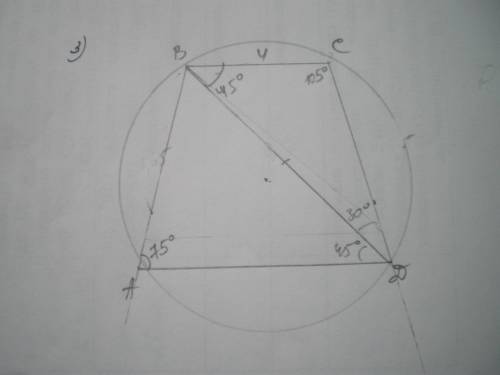
5. Трапеція включає два трикутника ABD и BСD. Коло, описане навколо трапеції, описане навколо обох цих трикутників. Отже, коло, описане навколо трапеції - це коло, описане навколо трикутника ВСD.

∠CBD = ∠BDA = 45° як внутрішні різносторонні кути при AD ║ ВС і січній BD.

За теоремою синусів ВС/sin30 = СD/sin45

CD = BC/(√2/2) = ВC·√2 = 4√2 см.

ВС/sin30 = 2R; R = BC/(2·(1/2)) = ВC = 4 см.