Радиус основания и образующая конуса равны соответственно 3 и 6. Найти высоту.

👇

Ответ:

samigyllin

19.09.2022

Объяснение:

Радиус основания, образующая конуса и высота - прямоугольный треугольник где образующая - гипотенуза (6), катеты - радиус (2) и высота (х);

по т. Пифагора высота - √(6²-3²)=√27=3√3 ед.

4,4(44 оценок)

Открыть все ответы

Ответ:

uefip

19.09.2022

1) 25

2) 15,625

3)1,2

Объяснение:

1. Площади подобных треугольников относятся как квадрат коэффициента подобия.

Т.к. стороны A₁ B₁ C₁ в 2 раза меньше сторон ABC, то коэффициент подобия равен 2, =>

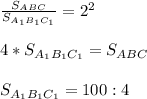
$\frac{S_{ABC}}{S_{A_{1}B_{1}C_{1}}} = 2^{2}\\\\4*S_{A_{1}B_{1}C_{1}} = S_{ABC}\\\\S_{A_{1}B_{1}C_{1}} = 100 : 4$

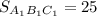$S_{A_{1}B_{1}C_{1}} = 25$ (см²)

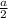2) Пусть сторона большого куба равна , тогда по условию сторона меньшего куба равна $\frac{a}{2}$ .

Объем большого куба: 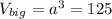$V_{big} = a^{3} = 125\\\\$ (см³)

Объем меньшего куба: 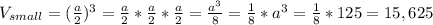$V_{small} = (\frac{a}{2} )^{3} = \frac{a}{2} * \frac{a}{2} *\frac{a}{2} = \frac{a^{3}}{8} = \frac{1}{8}*a^{3} = \frac{1}{8} * 125 = 15,625$ (см³)

3) Матрешку можно рассматривать как цилиндр.

Формула массы цилиндра: 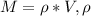$M = \rho * V, \rho$ - плотность материала, 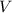- объем цилиндра.

Формула объема цилиндра: 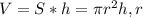$V = S*h = \pi r^{2}h, r$ - радиус основания, 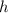- высота цилиндра.

Если меньшая матрешка вдвое меньше большей, то делаем вывод что высота большей матрешки вдвое больше высоты меньшей матрешки, а также радиус основания большей матрешки вдвое больше радиуса основания меньшей матрешки.

Пусть - радиус основания меньшей матрешки, 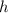- высота меньшей матрешки, тогда по формуле:

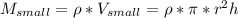$M_{small} = \rho*V_{small} = \rho*\pi*r^{2}h$ ;

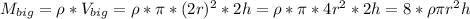
$M_{big} = \rho*V_{big} = \rho*\pi*(2r)^{2}*2h = \rho*\pi*4r^{2}*2h = 8*\rho\pi r^{2}h$

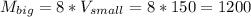$M_{big} = 8*V_{small} = 8 *150 = 1200$ (г) = 1,2(кг)

4,8(94 оценок)

Ответ:

OligCh

19.09.2022

Объяснение:

вы должны рассматривать высоту как катет прямоугольного треунольника. сначала начертите призму . проведите диагональное сечение . потом проведя диагональ самой призмы вы увидите что сечение разбивается на два прямоугольных треугольника .

ABCDA1B1C1D1 призма

BDB1D1 диагональное сечение

BD1 диагональ призмы.

по правилам прямоугольного треугольника если угол=30' то противоположный катет равен половине гипотенузы

по условию задачи гипотенуза это диагональ BD1

а катет равный половине гипотенузы это диагональ основания BD

в основание квадрат =>BD= 4V2 (V корень кв.)

BD1= 2*4V2=8V2

по теореме Пифагора DD1^2=(8V2)^2-(4V2)^2= 96

DD1=4V6

надеюсь правильно

4,6(11 оценок)