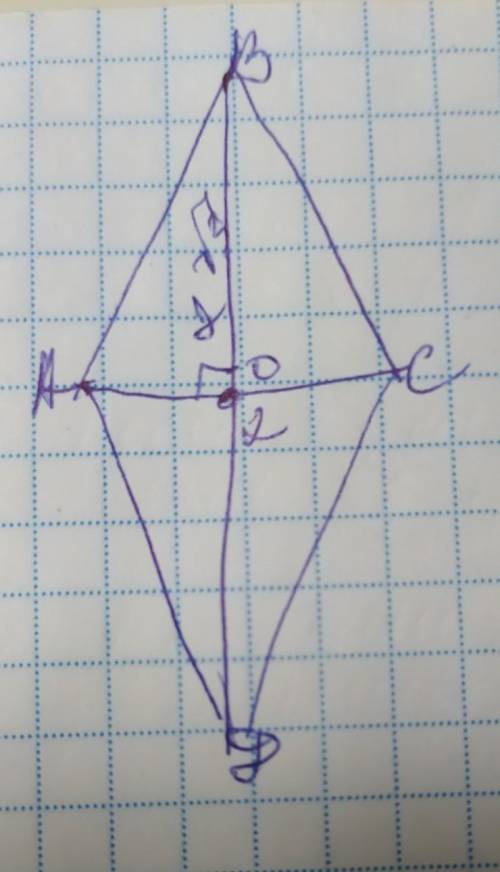
<А=<С=120°, <В<Д=60°
Объяснение:
обозначим вершины ромба А В С Д с диагоналями АС и ВД а точку их пересечения О. Диагонали ромба пересекаясь делятся пополам под прямым углом, образуя 4 равных прямоугольных треугольника, а также противоположные углы ромба равны и диагонали при пересечении делят углы из которых они проведены, пополам, поэтому АО=СО=2÷2=1см, ВО=ДО=2√3÷2=√3см
Теперь найдём угол через тангенс угла АВО. Тангенс угла - это отношение противолежащего от
угла катета к прилежащему:
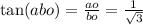
tg 1/√3=30°- это половина угла В,
Тогда <В=<Д=30×2=60°
Сумма углов ромба, прилегающие к одной стороне, составляет 180°, поэтому <А=<С=180–60=120°
обращаю внимание что 1/√3=√3/3, поскольку 1/√3 - это сокращённая дробь от √3/3. В тригонометрической таблице указано именно √3/3
Нам дана прямая а и некоторая точка М, которая не лежит на этой прямой. Нам
нужно доказать, что все прямые, которые проходят через точку М и пересекают
прямую а лежат в некоторой единственной плоскости.
Мы знаем, что в силу 1 теоремы через прямую а и точку М проходит
единственная плоскость, обозначим через. Теперь возьмем произвольную
прямую, которая проходит через точку М и пересекает прямую а, например, в
точке А. Прямая МА лежит в плоскости α, потому что две ее точки М и А, лежат в
этой плоскости. Значит, и вся прямая лежит в плоскости, в силу 2 аксиомы.
Итак, мы взяли произвольную прямую, которая удовлетворяет условиям задачи,
и доказали, что она лежит в плоскости α. Значит, все прямые, проходящие через
точку М и пересекающие прямую а лежат в плоскости α, что и требовалось
доказать
Объяснение:
есть свойство, что биссектриса любого угла треугольника делит противолежащую сторону на отрезки пропорциональные сторонам
BK:KC=AB:AC
4:3=16:AC
AC=3*16:4=48:4=12