Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Пусть дан отрезок ВС.
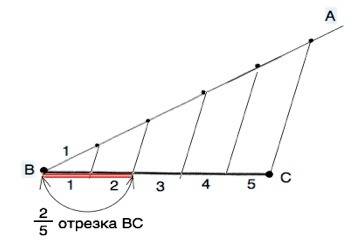
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
Объяснение:
Доказательство: Пусть даны две прямые a и b. Предположим, что они имеют более одной общей точки - точки M и N. Тогда через две точки M и N проходила бы не одна, а две прямые - прямые a и b. Но это противоречит аксиоме. Конец доказательства.
Что мне не нравится в доказательстве: Хорошо, мы доказали, что две разные прямые не могут иметь две общие точки. Но для меня ситуация выглядит так, что мы доказали только этот частный случай. А если мы возьмем три общие точки или больше? Не похоже, чтобы аксиома запрещяла, чтобы две разные прямые имели три общие точки.
Умом-то я понимаю, что если две прямые имеют более одной общей точки, то они являются одной и той же прямой. Но вот строго доказать, увы, не могу. И мне кажется, что для этого хватит все той же аксиомы. А вся моя проблема проистекает из-за неверного понимания самой аксиомы, которая скорее всего запрещяет и случаи с большим количеством общих точек.
МОЛОДЦЫ ДЕРЖИТЕСЬ УДАЧИ ВАМ -^-)
я хз окупації я довжина ето знать а
Объяснение:
оащеі