R = 30 ед.
Объяснение:
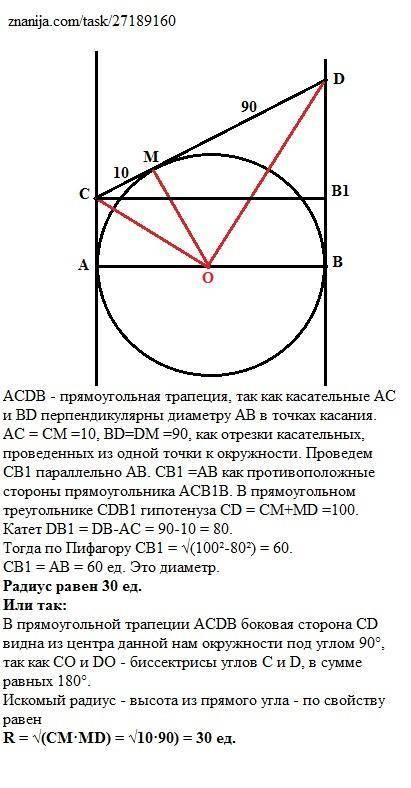
ACDB - прямоугольная трапеция, так как касательные АС и BD перпендикулярны диаметру АВ в точках касания.
АС = СМ =10, BD=DM =90, как отрезки касательных, проведенных из одной точки к окружности.
Проведем СВ1 параллельно АВ.
СВ1 =АВ как противоположные стороны прямоугольника АСВ1В. В прямоугольном треугольнике CDB1 гипотенуза CD = СМ+MD =100 ед.
Катет DB1 = DB-АС = 90-10 = 80ед.
Тогда по Пифагору СВ1 = √(100²-80²) = 60ед.
СВ1 = АВ = 60 ед. Это диаметр.
Радиус равен 30 ед.
Или так:
В прямоугольной трапеции АСDB боковая сторона CD видна из центра данной нам окружности под углом 90°, так как СО и DО - биссектрисы углов C и D, в сумме равных 180°.
Искомый радиус - высота из прямого угла - по свойству равен
R = √(CM·MD) = √10·90) = 30 ед.
Объяснение:
Я не очень поняла саму задачу, прости, не могу