Відповідь:
3 см
Пояснення:
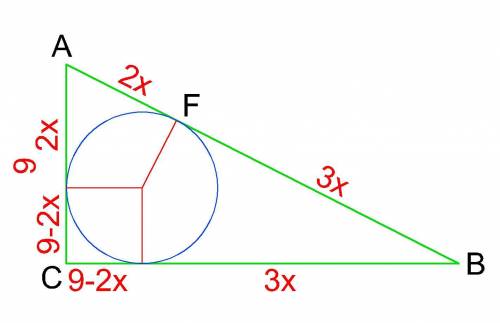
Відомо, що коло, вписане в трикутник, точками дотику до сторін відділяє рівні відрізки зі сторони кожної вершини.
Також відомо, що висоти - радіуси, проведені із центра такого кола в прямокутному трикутнику до катетів утворюють з відрізками від точок дотику до вершини прямого кута квадрат зі стороною, рівною радіусу вписаного кола.
Згідно з умовою, позначимо AF як 2x, FB як 3x, тоді
r=9-2x
За теоремою Піфагора складемо рівняння:
9²+ (9-2х+3х)²=(2х+3х)²
81+(9+х)²=25х²
81+81+18х+х²-25х²=0
24х²-18х-162=0
4х²-3х-27=0
Дискрімінант: Д=9+4*4*27=441=21²
х₁=(3+21)/8=3 см
х₂=(3-21)/8=-2.25 см (не підходить).
Тоді r=9-2·3=3 см
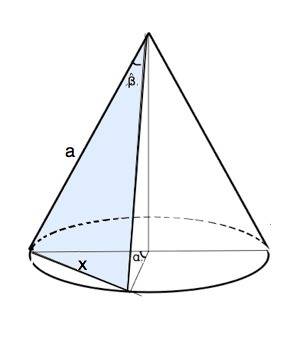
Через вершину конуса с основанием радиуса R проведена плоскость, которая пересекает его основание по хорде, которую видно из центра основания под углом α, а из вершины – под углом β. Найти площадь сечения.
--------
Данное сечение конуса - равнобедренный треугольник. Пусть сторона этого треугольника равна а.
Тогда его площадь можно выразить S=a²•sinβ/2.
1) Примем длину хорды равной х. Тогда из треугольника в основании, образованного хордой и двумя радиусами, квадрат её длины можно выразить по т.косинусов.
х²=2R²-2R²•cosα=2R²(1-cosα)
2) Выразим квадрат длины хорды по т.косинусов из треугольника в сечении:
х²=2а²-2а²•cosβ=2а²(1-cosβ)
3) Приравняем найденные значения х²
2R²(1-cosα)=2а²(1•cosβ)
Выразим а² из этого уравнения:
а²=R²(1-cosα):(1-cosβ)
Отсюда
S сечения=[R²(1-cosα):(1-cosβ)]•sinβ:2
Відповідь: см,
см,  см,
см,  см
см
Пояснення:
Нехай бічна сторона х, тоді основа трикутника- (х +2). Периметр трикутника- то сума усіх його сторін.
х+2+х+х=28
3х=28-2
3х=26
х+2= (см)- основа трикутника
(см)- основа трикутника