ответ: 432π
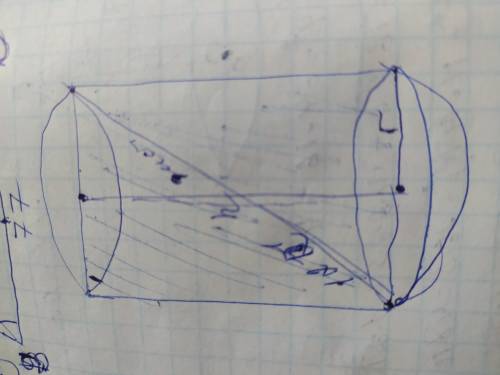
Объяснение: обозначим радиус r, a высоту h. Если r/h=1/2, то: h=2r. 2 радиуса
- это диаметр, и диаметр основания равен высоте. Высота, радиус и диагональ осевого сечения цилиндра образуют равнобедренный прямоугольный треугольник, в котором диаметр основания и высота являются катетами а диагональ гипотенузой. В равнобедренном прямоугольном треугольнике гипотенуза больше катета в √2 раз, поэтому h=диаметру=12√2/√2=
=12, тогда радиус=12/2=6
Найдём площадь основания по формуле:
Sосн=πr²=π×6²=36π
Теперь найдём объем цилиндра зная его площадь основания и высоту по формуле: V=Sосн×h=36π×12=432π(ед³)
Для конуса известны 2 соотношения:
S бок=πRL
φ=360R/L
где R- радиус основания, L- образующая конуса.
Из первого соотношения находим RL:
240π=πRL
RL=240
Из второго соотношения выражаем L через R:
120=360R/L
L=3R
3R²=240
R²=80
R=√80=4√5 cм
L=12√5 см
Находим площадь полной поверхности конуса:
S полн.=πR(L+R)=4π√5(12√5+4√5)=4π√5*16√5=320π см²
Можно оставить так, если надо числовое значение, то будет ≈1004,8 см²
А о каком шаре идёт речь в условии, я не знаю... ;)
P.S. Ну и, я надеюсь, ты не забудешь отметить это как "Лучшее решение"?!.. ;))