ч. т. д.
Объяснение:
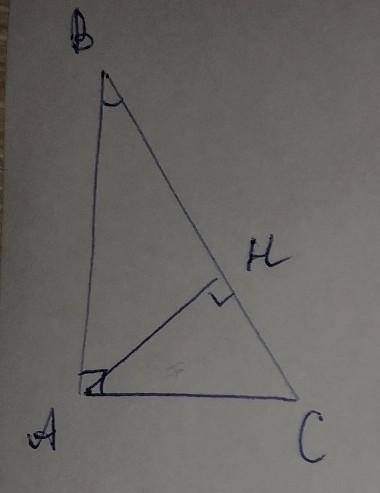
Дано: треугольник АВС, угол ВАС=90°, АН - высота.
Доказать: 4АН=ВС
Доказательство:
1. Рассмотрим тр-к АВС (угол А=90°): sinABC=sin15°=AC/BC, тогда BC=AC/sin15°;
2. Тр-к ВАС подобен тр-ку АНС по двум углам (т. к. АН - высота, угол АНС=90°=уголВАС; угол ВСА - общий).
Из подобия тр-ков следует равенство соответствующих углов: уголНАС=уголАВС=15°
3. Рассмотрим тр-к АНС (уголАНС=90°): cosHAS=cos15°=AH/AC, следовательно, AC=AH/cos15°.
4. АН/ВС=АН/(АС/sin15°)=AH/((AH/cos15°)/sin15°) =sin15°cos15°=2sin15°cos15°/2=sin30°/2=0,5/2=0,25
AH/BC=0,25=1/4, следовательно, 4АН=ВС
ч. т. д.
1) По стороне правильного треугольника можно его вычислить площадь:
S = a²√3 / 4 = (16√3)² · √3 / 4 =64√3 см²
высота этого треугольника:
h = a√3 / 2 = 16 · √3 · √3 / 2 = 24 см
треть высоты:
r = 24 ÷ 3 = 8 см (радиус вписанной в него окружности)
Высота пирамиды, апофема и радиус вписанной в основание пирамиды окружности образуют прямоугольный треугольник:
17² = 8² + H² (теорема Пифагора), где H - высота пирамиды:
H² = 17² - 8² = (17 - 8)(17 + 8) = 9 · 25 ⇒ H = 15 см
V = 1/3 · Sосн · H = 1/3 · 64√3 · 15 = 320√3 см³