Равнобедренный треугольник с высотой ам = 25 см и основанием вс вписан в окружность радиусом 17 см. найдите сторону ав этого треугольника

👇

Ответ:

1941108

19.11.2022

ΔАВС- ранобедренный, значит АМ является и медианой и высотой, следовательно является и серединным перпендикуляром к ВС. Известно, что центр описанной окружности — точка пересечения серединных перпендикуляров.

Значит центр окружности (на рисунке точка О) лежит на высоте АМ.

АМ=25 см, ОА=ОС=17 см ОМ=8 см

Ну и далее, собственно, вычисления, всё по т. Пифагора:

$CM=\sqrt{OC^2-OM^2}=\sqrt{17^2-8^2}=\sqrt{289-64}=\sqrt{225}=15\\CM=BM\\AB=\sqrt{BM^2+AM^2}=\sqrt{15^2+25^2}=\\\\=\sqrt{225+625}=\sqrt{850}=5\sqrt{34}$

И, если не трудно, не забудь нажать "Лучшее решение", ОК?!.. ;))

4,5(74 оценок)

Открыть все ответы

Ответ:

Felua

19.11.2022

Не верное утверждение Г.

Объяснение:

А) Прямоугольные треугольники с соответственно равными острыми углами (а даже и с одним, так как второй - прямой) ПОДОБНЫ. Отношение площадей подобных фигур равно квадрату коэффициента подобия (отношению линейных размеров). Значит отношение гипотенуз равно √(2/3). Утверждение верное.

Б) Диагональ трапеции делит ее на два треугольника с одинаковой высотой, следовательно их площади относятся, как их основания, к которым проведена эта высота. Утверждение верное.

В). Медиана треугольника делит треугольник на два треугольника, у которых равны и основания, и высоты. Значит и их площади равны. Утверждение верное.

Г). Периметры равновеликих треугольников в общем случае НЕ равны. (Предыдущий пример с медианой, когда треугольник не равнобедренный - периметры разные). Утверждение НЕ верное.

4,4(13 оценок)

Ответ:

MaxKryaks

19.11.2022

Точка О2 - центр вписанной окружности в тр-ник АВС. Точка О1 - центр заданной окружности.
Около тр-ка АВС опишем окружность.
АО2, ВО2 и СО2 - биссектрисы соответствующих углов.
Продолжим отрезок СО2 до пересечения его с описанной окружностью в некой точке К.
∠АО2К=∠А/2+∠С/2, т.к. ∠АО2К является внешним к тр-ку АСО2.
∠ВАК=АВК=∠С/2, т.к. оба опираются на те же дуги, на которые опираются равные углы из вершины тр-ка АВС. КА=КВ по этой же причине.
Заметим, что в тр-ке АКО2 ∠КАО2=∠АО2К, значит он равнобедренный.
КА=КО2=КВ, значит точка К - центр описанной около тр-ка АВО2 окружности.
Тр-ник АВС - равнобедренный. В нём СМ - биссектриса и высота. В прямоугольном тр-ке АСМ ∠А+∠С=90°. Заметим, что и в тр-ке АСК ∠САК=90°, значит ∠CВК=90°. СА и CВ - касательные к окружности с центром в точке К. Точки А и В лежат на этой окружности. Но СА и CВ - касательные к заданной окружности, значит точки К и О1 совпадают.
О1О2 - радиус заданной окружности, значит центр вписанной в тр-ник АВС окружности лежит на данной окружности.
Доказано.
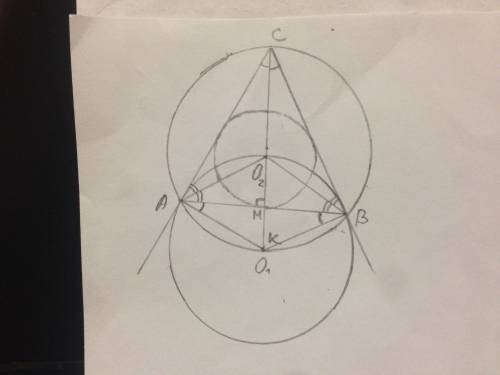
Две прямые, касающиеся данной окружности в точках а и в, пересекаются в точке с. докажите, что центр