Дано :
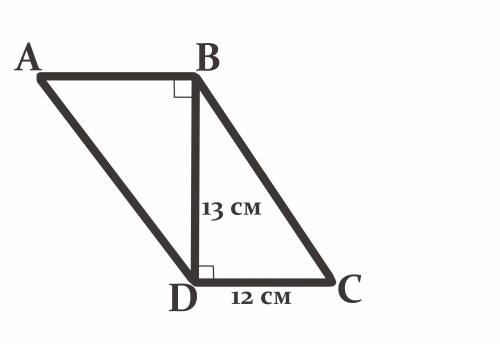
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
из точки В к основанию АД опускаешь высоту, получается высота ВК.
из точки С опускаешь высоту к основанию АД, получается высота СМ.
ВСМК-прямоугольник, значит ВС=КМ=4. Из АД-КМ=18-4=14
АК=МД=14/2=7
В прямоугольном треугольнике, против угла 30 градусов, лежит катет равный половине гипотенузы.
В треугольнике АВК угол А 60 градусов(по условию), угол К 90 градусов(ВК высота), значит угол В=180-(90+60)=30
Катет АК лежит против угла В, то есть против угла 30 градусов, отсюда следует: АВ=2хАК=2х7=14