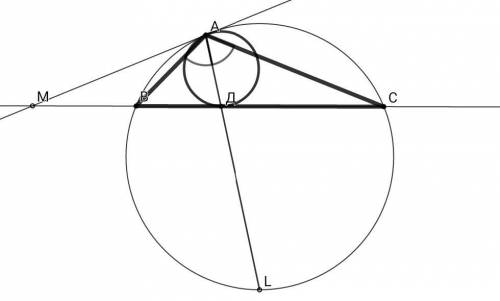
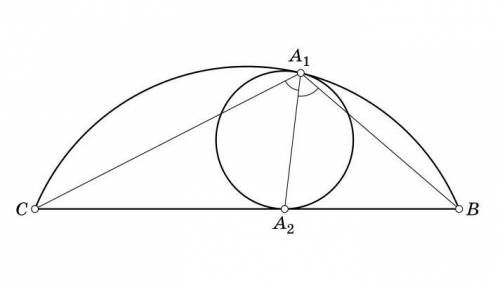
Докажем лемму Архимеда через дополнительное построение. Проведём к окружностям общую касательную АМ, пересекающая прямую ВС в точке М. Пусть ∠BAD = α, ∠CAD = β, ∠ACB = γ, тогда ∠ВАМ = ∠АСВ = γ (по свойству угла между касательной МА и хордой АВ), ∠MAD = γ + α, ∠ADB = ∠CAD + ∠ACD = β + γ (по свойству внешнего угла ΔACD). MA и MD - касательные к малой окружности ⇒ МА = MD - как отрезки касательных, ΔAMD - равнобедренный, ∠MAD = ∠MDA ⇒ γ + α = β + γ ⇒ α = β , AD - биссектриса ∠ВАС, ч.т.д. Конечно, данную лемму можно доказать в 2 строчки, заметив гомотетию окружностей, но это дело вкуса.
Даны точки: А(4; 0) и В(0; 2). Также известно, что центр О окружности расположен на оси Oy. Примем координаты О(0; у).
Далее приравниваем длины радиусов: ОА = ОВ.
Удобнее в квадрате: ОА² = ОВ².
4² + у² = (2 - у)²,
16 + у² = 4 - 4у + у²,
4у = -16 + 4 = -12.
у = 12/4 = -3.
Получена ордината центра. Точка О(0; -3)
Радиус R = 2 - (-3) = 5.
ответ: уравнение окружности x² + (y + 3)² = 5².