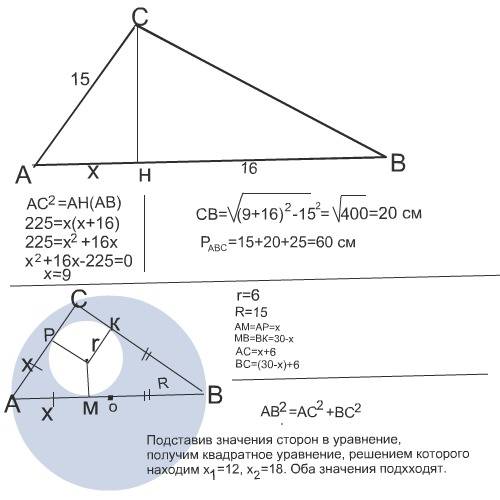
1)Пусть ABC — данный треугольник (угол C — прямой, AC = 15); CD — высота; BD = 16. Обозначим BD = x. Из подобия треугольников ABC и ACD (угол A общий, ⁄ ADC = ⁄ ACB = 90°) получаем
2)
Пусть а и в катеты треугольника, тогда с=30, т.к. радиус описанной окружности равен половине гипотенузы r=p-c,p=r+c=36, P=36*2=72,a+b=72-30=42.имеем
{а+в=42
a^2+b^2=900
{a^2+b^2=2*ab=42^2=1764
a^2+b^2=900
{900+2*ab=1764
2ab=1764-900
{a+b=42
ab=432
a^2-42a+432=0
а1=18,а2=24
в1=24, в2=18
Как правило, при решении задач по геометрии нужно сделать рисунок. Сделаем рисунок к задаче.
Проведем через центр О окружности высоту КН трапеции. Соединим центр с вершинами С и Д углов трапеции. ОС=СД=радиусу окружности.
Дальше все просто. По теореме Пифагора ( или приняв во внимание, что получилось два "египетских" треугольника), найдем сначала ОД, затем ОК ( расстояние от центра окружности до меньшего основания трапеции).
Высота трапеции равна сумме расстояний от центра окружности до оснований и равна:
3+4=7