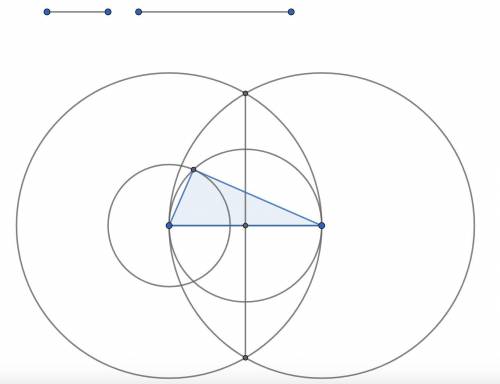
Построим прямоугольный треугольник с циркуля и линейки. Случай, когда данные стороны равны, рассматривать не будем, ибо в таком случае одна из них не может быть равна катету, а другая — гипотенузе.
1. На большей стороне (гипотенузе, назовём её b) построим две окружности с центрами в концах отрезков и радиусом b. Проведём прямую через точки пересечения окружностей. Она будет пересекать гипотенузу в середине в силу симметричности чертежа.
2. Построим окружность с центром в середине гипотенузы и радиусом b / 2. Тогда эта окружность будет содержать концы отрезка, который будет являться для неё диаметром.
3. Построим окружность с центром в одном из концов гипотенузы (не теряя общности — в левом конце) и радиусом, равному меньшей стороне (катету, назовём его a). Отметим точку пересечения с окружностью, построенной в п. 2.
4. Проведём отрезок, соединяющий правый конец гипотенузы и точку пересечения окружностей (см. п. 3). Полученный треугольник (выделен на рисунке) будет прямоугольным, так как он вписан в окружность, один из его углов опирается на диаметр, то есть угол прямой.
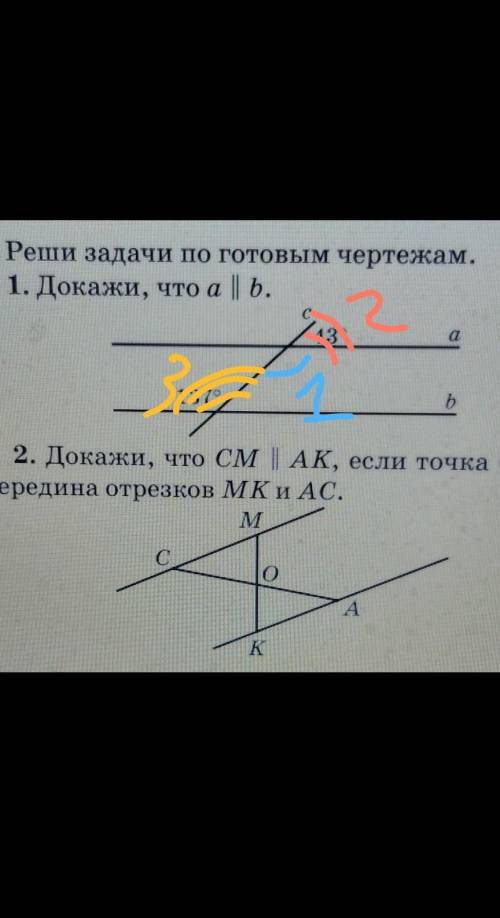
Объяснение:
#1
Угол 1 и угол 2 смежные. Сумма смежных углов равна 180 градусов => 180-43=137°-угол
Угол 3=углу 1 => угол 1 и угол 3-накрест.леж=> а||б по признаку накрест.леж углов
#2
Рассмотрим треугольники СОМ и КОА
1. Угол СОМ=углу КОА, тк вертикальные
2. МО=ОК, тк т.О середина отрезка МК
3. СО=ОА, тк т.О середина отрезка АС => треугольник СОМ=треугольнику КОА по двум сторонам и углу между ними
В равных треугольниках соответствующие элементы равны => угол КАО=углу ОСМ
Угол КАО и угол ОСМ -накрест.леж=> СМ||АК по признаку накрест.леж углов