Question

Бічні грані правильної шестикутної піраміди нахилені до основи під кутом 30°. Радіус кола, описаного навколо основи 5 см. Знайти площу бічної поверхні. А) 50 см2 Б) 75 см2 В) 100 см2 В) 120 см2

Answer 1

S бічної поверхні =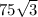 $75\sqrt{3}$ сантиметрів квадратних

Объяснение:

Дано:  Правильна шестикутна піраміда, R = 5 см, α = 30°(α - бічні грані правильної шестикутної піраміди нахилені до основи під кутом α)

Знайти:

S - ?(площу бічної поверхні)

Розв'язання: Розглянемо правильний шестикутник ABCDEF. Проведемо відрізки OD і OE і розглянемо трикутник Δ DOE, який буде рівнобедренним тому, що OD = OE (OD = OE = 5см за умовою), як радіуси описаного кола.Позначимо середину відрізка DE у точці M і з вершини O проведемо відрізок OM - який буде медіаною. За умовою ∠HMO = α.За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, а так як OM⊥DE, то OM є радіусом вписаного кола.У правильного шестикутника 6 сторін, а отже шість центральних кутів, нехай центральний кут β, тоді ∠DOE = β, усі 6 центральних кутів утворють повне коло отже ∠DOE = β =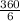 $\frac{360}{6}$ = 60°.

Так як OM - бісектриса за властивістю рівнобедренного трикутника, то

∠DOM = ∠MOE = ∠DOE : 2 = 60° : 2 = 30°.OM є висотою, тоді

sin ∠MOE =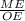 $\frac{ME}{OE}$ ⇒ ME = OE * sin ∠MOE = 5 * 0,5 = 2,5 см.Так як за OM - медіана, то DE = 2DM = 2ME = 2 * 2,5 = 5 см.

cos ∠MOE =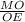$\frac{MO}{OE}$ ⇒  MO = cos ∠MOE * OE = cos 30° * OE = $\frac{5\sqrt{3} }{2}$ = $2,5\sqrt{3}$

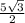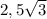
Проведемо відрізок OH - який буде висотою за властивісью шестикутної піраміди.РозглянемоΔ MOH.

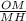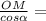
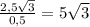cos ∠MOH = cos α = $\frac{OM}{MH}$  ⇒ MH = $\frac{OM}{cos \alpha } =$$\frac{2,5\sqrt{3} }{0,5}=5\sqrt{3}$ .

За властивістю правильної піраміди усі її грані є рівними рівнобедренними трикутниками, отже Δ HDE - рівнобедренний.Проведемо відрізок HM - який є медіаною так як DM = ME, За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, отже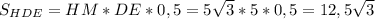 $S_{HDE} = HM * DE *0,5 = 5\sqrt{3} * 5 * 0,5 = 12,5\sqrt{3}$.

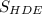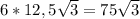S бічної поверхні = 6 * $S_{HDE}$ = $6 * 12,5\sqrt{3}= 75\sqrt{3}$.