Дано: равнобедренный треугольник PKN
KN-основание,PM-медиана,
Доказать: KON-равнобедренный
Первый вариант Доказательство
Рассмотрим треугольники KOM и NOM
OM-общая
KM=MN-так как PM медиана и проходит к середине основания
По свойству биссектрисы равнобедренного треугольника, она является медианой и высотой,
углы KOM=MON- т.к. PM высота
Значит эти треугольники равны по первому признаку.
Исходя из равенства треугольников KOM и MON,следует что они образуют равнобедренный треугольник при их совмещении ч.т.д.
Второй вариант Доказательство
В треугольнике KOM OM является биссектрисой по равенству углов KOM и MON
В треугольнике KOM OM является медианой т.к. делит основание KN на 2 равные части и образует прямой угол
Такое явление характерно свойству равнобедренных треугольников, значит то что KON равнобедренный ч.т.д.
1) Формула объёма конуса V=S•H:3=πr²H:3
Формула объёма шара
V=4πR³:3
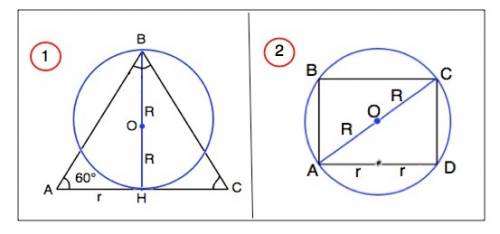
Осевое сечение данного конуса - равносторонний треугольник, т.к. его образующая составляет с плоскостью основания угол 60°.
Выразим радиус r конуса через радиус R шара.
r=2R:tg60°=2R/√3
V(кон)=π(2R/√3)²•2R²3=π8R³/9
V(шара)=4πR³/3
V(кон):V(шар)=[π8R³/9]:[4πR³/3]=(π•8R³•3/9)•4πR³=2/3
———————
2) Формула объёма цилиндра
V=πr²•H
Формула площади осевого сечения цилиндра
S=2r•H
Разделим одну формулу на другую:
(πr²•H):(2r•H)=πr/2⇒
96π:48=πr/2⇒
4π=πr
r=4
Из площади осевого сечения цилиндра:
Н=S:2r=48:8=6
На схематическом рисунке сферы с вписанным цилиндром
АВ- высота цилиндра, ВС - его диаметр,
АС - диаметр сферы.
АС=√(6²+8²)=√100=10
R=10:2=5
S(сф)=4πR8=4π•25=100π см²
Так как АВ больше высоты цилиндра, АВ наклонная, она и ось цилиндра лежат в разных плоскостях и не пересекаются. Они - скрещивающиеся прямые.
Цитата:"
Для нахождения расстояния между скрещивающимися прямыми нужно:
- Найти плоскость, перпендикулярную одной из скрещивающихся прямых;
- Ортогонально спроектировать вторую прямую на эту плоскость;
- Из точки пересечения плоскости первой прямой опустить перпендикуляр на проекцию второй прямой."
Ось цилиндра перпендикулярна плоскости основания. Расстоянием между АВ и осью цилиндра будет отрезок, проведенный перпендикулярно от центра основания к проекции АВ.
Обозначим центр основания О. Опустим перпендикуляр ВК к основанию.
Хорда АК - проекция АВ на плоскость основания. ОА=ОК -радиусы. Треугольник АОК - равнобедренный. ОН - его медиана и высота. ⇒
АК- катет прямоугольного ∆ АВК и по т.Пифагора равен 8 ( его стороны составляют одну из троек Пифагора)
АН=АК:2=4
∆ АОН прямоугольный, отношение АН:ОА=4:5 - это "египетский" треугольник, и искомое расстояние ОН=3 ( можно проверить по т.Пифагора).