Уравнение окружности имеет вид , где и - координаты центра окружности, а - её радиус.
Координаты центра заданной окружности (2; 6).
1. То, что окружность касается оси Ох, значит, что её радиус равен расстоянию от центра окружности до оси абсцисс. На оси Ох ордината равна нулю, а значит, радиус окружности равен 6. Таким образом, уравнение окружности в этом случае: .
2. То, что окружность касается оси Оy, значит, что её радиус равен расстоянию от центра окружности до оси ординат. На оси Oy абсцисса равна нулю, а значит, радиус окружности равен 2. Таким образом, уравнение окружности в этом случае: .
Построим к данной задаче рисунок. 1. Строим окружность с центром О. 2. Проведем диаметр в этой окружности ВС. 3. На окружности ставим точку А. 4. точку А соединим с Точками А и В. ΔАВС- прямоугольный, ∠ВАС - вписанный, опирается на диаметр. ∠ВАС=90°ю 5. С точки А опускаем перпендикуляр АD на диаметр ВС. 6. Проводим радиус АО. Теперь переходим к решению задачи. По условию длина окружности равна 2πR=52π: 2R=52; R=52/2=26 см. ΔАОВ - равнобедренный; ОВ=ОА=26 см. ΔАОD - прямоугольный, по теореме Пифагора ОD²=ОА²-АD²=26²-24²=100; ОD=√100=10 см. ВD=ОВ+ОD=26+10=36 см. СD= ОС+ОD=26-10=16 см. ответ: 16 см; 36 см.
Для того, чтобы охранять природу человеку необязательно вступать в организации, достаточно ставить низкую температуру при стирке, чтобы сохранять энергию, а также не пользоваться лифтом или делать это редко, такая мера также позволит электроэнергию. нужно чаще использовать велосипед, а не автомобиль или общественный транспорт, это позволит энергию и делать меньше выбросов газов в атмосферу. можно использовать энергосберегающие лампы и потом сдавать их, а также использовать бумагу из вторичного сырья и прочее.
Уравнение окружности имеет вид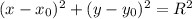 , где
, где 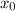 и
и 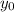 - координаты центра окружности, а
- координаты центра окружности, а 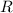 - её радиус.
- её радиус.
Координаты центра заданной окружности (2; 6).
1. То, что окружность касается оси Ох, значит, что её радиус равен расстоянию от центра окружности до оси абсцисс. На оси Ох ордината равна нулю, а значит, радиус окружности равен 6. Таким образом, уравнение окружности в этом случае: .
.
2. То, что окружность касается оси Оy, значит, что её радиус равен расстоянию от центра окружности до оси ординат. На оси Oy абсцисса равна нулю, а значит, радиус окружности равен 2. Таким образом, уравнение окружности в этом случае: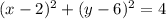 .
.